Kinematics of Differential Drives
Instantaneous Center of Rotation
In a connected drive system (like a car), all wheels have to move along a circle.
If travelling forward, the circle is infinely large.
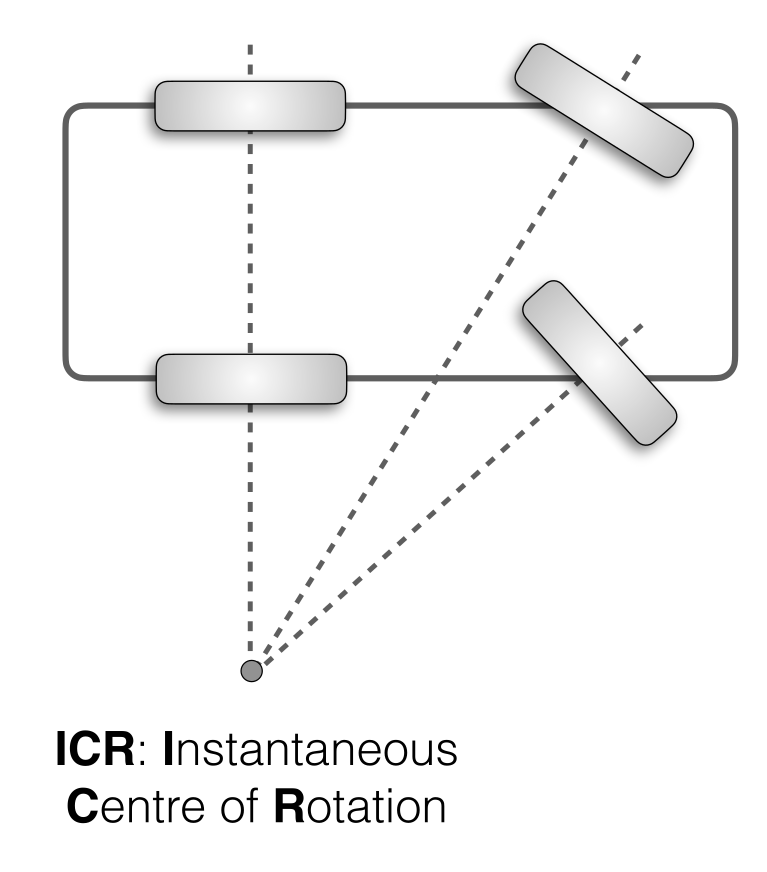
The centre of this turning circle is the convergence of all of the axels. This point is the ICR (Instantaneous Centre of Rotation)
Differential Drive
- $R$
- This is the radius of the current turning circle of the robot. The radius of the ICR.
- $\omega$
- This is the rotational velocity, about the ICR, of the robot $\omega=\frac{\Delta \theta}{\Delta t}$.
- $l$
- The distance between the wheels of the robot.
Forward Velocity of the Robot
\[\begin{aligned} v &= \omega R\\ v &= \frac{v_r+v_l} 2 \end{aligned}\]Velocities of the Wheels
\[\begin{aligned} v_l&=\omega(R-\frac l 2)\\ v_r&=\omega(R+\frac l 2)\\ \end{aligned}\]ICR Radius
\[R=\frac l 2\times \frac{v_l+v_r}{v_r-v_l}\]Rotational Velocity
\[\omega = \frac{v_r-v_l} l\]If the wheel velocities are equal then $\omega = 0$ and the robot moves forward.
Rotation Matrix
A rotation matrix is used to perform a rotation in Euclidean space. The following function rotates counter-clockwise through angle $\theta$ around the origin:
\[R(\omega)= \begin{bmatrix} \cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix}\]We can use this to rotate a coordinate as a vector:
\[\begin{aligned} \begin{bmatrix} x'\\y' \end{bmatrix} =& \begin{bmatrix} \cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix}\\ =& \begin{bmatrix} x\cos(\theta) & -y\sin(\theta)\\ x\sin(\theta) & y\cos(\theta) \end{bmatrix} \end{aligned}\]Differential Drive - Kinematics
To determine where the robot is, given an angular momentum $\omega$ after $\delta t$, wie can use the rotation matrix:
- Translate the ICR to the origin (subtract the coordinates of the ICR from the robot position $(x,y)$).
- Apply the rotation matrix.
- Reposition the final location, taking into account the original ICR location.
- Add the angular distance $\omega\delta t$ to the robot’s orientation.