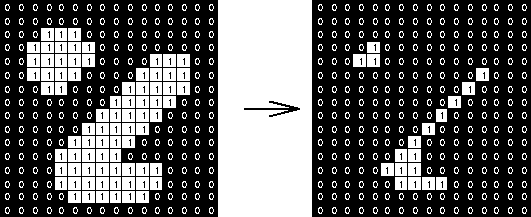Digital Images
Discrete representation of spatial and intensity values in a 2D matrix.
Raw images are often:
- Extremely noisy
- Contain invisible bands of the EM spectrum.
- Contain too much information (that needs to be cropped out)
Image Sensing & Optics
Images are a signal so it is collected using a sensor.
- Light is reflected off, or emitted by, objects.
- Photos pass through the optics.
- Photos are focussed onto the focal plane.
- Electronically or chemically.
- The energy of photos is importance when forming images.
Not all images are in the visible spectrum so we can use other wavelengths, ultrasonic and so on to create images.
Attenuation

IR Cameras
They are good when there isn’t a large amount of ambient light.
There are three different types of IR:
- Near IR 0.7um - 2um
- Little thermal emission, but can use laser illumination.
- Mid-wave Infrared 3um - 5um
- Good for hot objects as there is less background thermal emission.
- Long-Wave Infrared 8um - 14um
- Good for room temperature (thermal LWIR emission peaks at 300K)
Low Light
Visible band cameras only work well when there is ambient light.
This means they are not good at night.
To correct for this we can use an amplifier:
- This introduces a lot of noise.
- Tends to make the camera sensitive to glare.
- MATLAB (licensed)
- Through image processing toolbox.
- ImageJ (free)
- OpenCV (free)
Typical Image Processing System
graph LR
pp[Pre-processing] --> mp[Main Processing]
mp --> pp2[Post-Processing]
Pre-Processing:
- Basic Correction
- Basic Noise Removal
- Background Removal
- Alignment
- Format Changing
- Transformation
Main Processing:
- Advanced Correction
- Advanced Noise removal
- Segmentation
- Detection
- Searching
- Feature Extraction
- Recognition
Post Processing:
- Image Formation
- Format Changing
- Result Representation
- Report Generation
You will gain significantly better results if you pre-process.
Terminology
- Field of View
- Total angle covered by the camera in a single image.
- Field of Regard
- Total angle that can be covered by the camera in a series of images.
- Focal Length (fl)
- Effective distance between lens and focal plane.
- Aperture (d)
- Effective size of the lens.
- Pixel
- Individual element of the image.
- F-number (fl/d)
- Measure of the light allowed through the lens.
- Gain-offset Correction
- Control of image exposure (gain) and removal of dark current (offset).
- Frame Rate
- Number of frames per second.
- Dioptre
- Optical power of a lens (same as $\frac 1 {\text{fl}}$)
Human Eye
The human eye has two optical components:
- The cornea has an optical strength of 31 dioptres.
- The lens is only 19 dioptres.
Rods & Cones
Rods:
- Sensitive to all types of light.
- About 100 times more sensitive to light than the cones.
Cones:
- Concentrated around the centre of the field of view.
- Come in three types:
- L (Long)
- M (Medium)
- S (Short)
Other animal often have limited colour vision due to a differing number of rods and cones.
Fovea & Saccades
The fovea is responsible for what we normally think of a human vision.
- The high resolution region of human colour vision is only 2 degrees.
Stereo Vision
Binocular vision relies on the two eyes having different views of the same scene.
The distance between the two cameras is called the baseline.
The fact that the two cameras can see different views is called parallax.
Empirical Condition:
\[\frac{\theta_A-\theta_B}{\theta_\text{FOV}}\times N_\text{Pixels}>1\]
Colour
Colour images are composed of three bands: R,G,B
Often it is better to use HSI (Hue, Saturation, Intensity) instead of RGB, as the three colour bands overlap. This causes a change in one band to effect the others.
It is possible to convert from one colour space to another (CMYK to RGB conversion). A formula should be provided if this is required.
Camera Resolution
Resolution is limited by pixels and the field of view.
A field of view of $\theta$ rads with $N$ pixels gives an angular resolution of:
\[\Delta\theta = \frac\theta N\]
Johnson Criteria
This is an empirical experiment that determines the ability to correctly detect and recognise objects.
- Detection (with 50% probability) = resolve 1 bar.
- Recognition (with 50% probability) = resolve 3 bar.
- Identification (with 50% probability) = resolve 5 bar.
1 bar is a minimum of 3 pixels.
Optical Effects
- Vignetting
- The shadowing of the corners of an image from the optical aperture (the effect of the finite focal length).
- Optical Distortion
- This is the effect of imperfect lenses. Barrel distortion expands towards the centre. Chromatic distortion presents itself as a prism effect.
- Image Noise
- Non-uniform response to stimulus across the focal plane.
- Blooming
- Where high intensity pixels leak into neighbours.
Binary Images
- Simplest type of images
- Each pixel can either be black or white
The size of the image is:
\[M\times N\text{ bits}\]
where $M$ and $N$ are the rows and columns.
A histogram for a 1 bit image only has two peaks for dark and light.
Grayscale Images
- Generally 8 bits per pixel
- This gives 256 levels of brightness.
Colour Images
- Each channel RGB has 8 bits.
- This gives 24 bits per pixel.
You can generate histograms for each channel or sum the channels to account for all of them.
Colour Quantisation
You can’t represent an infinite number of colours using 24 bits. As a result the raw colour is quantised to fit in the colour space.
We can use the following algorithms to add dithering to account for quantisation:
- Uniform
- Median-cut
- Octree
- Popularity
- Generalised Lloyd
Conversion
Colour Image to Grayscale Conversion
This can be achieved by converting each RGB pixel to greyscale by forming a weighted sum:
\[a_1R+a_2G+a_3B\]
MatLab’s rgb2gray uses $a_1 = 0.2989$, $a_2=0.5870$ and $a_3=0.1140$.
Grayscale to Binary Image Conversion
To convert from grayscale to binary we need a threshold value.
Thresholding is an easy way to:
- Convert grayscale to binary.
- Separate foreground from background.
There are two levels of thresholding:
- Histogram
- Multi-level Thresholding
We can complete image transformations using matrix operations.
Arithmetic Operations
These are pixel by pixel operations:
- Addition/Subtraction
- Multiplication/Division
- Logical Operations
We should scale the final output so that we don’t overflow/underflow. In MatLab we can use imadd, imsubtract etc.
These are combinations of:
-
Translation
\[\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}x_i\\y_i\end{bmatrix}\]
-
Scaling
\[\begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}S_x& 0\\0 &S_y\end{bmatrix}\cdot\begin{bmatrix}x\\y\end{bmatrix}\]
-
Roation
\[\begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\cdot\begin{bmatrix}x\\y\end{bmatrix}\]
We can put all transforms in the same format so we can combine them, to be used in one operation:
-
Translation
\[\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}1&0&x_i\\0&1&y_i\\0&0&1\end{bmatrix}+\begin{bmatrix}x_i\\y_i\\1\end{bmatrix}\]
-
Scaling
\[\begin{bmatrix}x'\\y'\\1\end{bmatrix} =\begin{bmatrix}S_x& 0&0 \\0&S_y&0\\0&0&1\end{bmatrix}\cdot\begin{bmatrix}x\\y\\1\end{bmatrix}\]
-
Roation
\[\begin{bmatrix}x'\\y'\\1\end{bmatrix} = \begin{bmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix}\cdot\begin{bmatrix}x\\y\\1\end{bmatrix}\]
Refer to slide 20 for 3D transformation matrices for:
- Translation
- Scaling
- Roll
- Pitch
- Yaw
3D transformations use 4 by 4 matrices.
Pixels, Neighbours & Connectivity
- $N_4$ Connectivity
- Each pixel has 4 pixels directly around it.
- $N_8$ Connectivity
- This includes diagonally adjacent pixels, so all pixels surrounding a pixel.
Structuring Element
This is a mask that can be used to define pixel neighbours:
- It is a small matrix of odd index.
1s in the matrix define pixels that are neighbours.
This type of structuring element is called flat.
- SEs don’t have to be square.
- SEs don’t have to be symmetrical.
- Non-flat SEs contain values that are non-binary.
Structuring Element Uses
They are used to probe large images for specific shapes:
- Therefore you should choose a SEs template to match the shape you want to find in the main image.
The size of the SE determines the detection scale:
- Smaller SE size, will discover more small features.
Distance Between Two Pixels
Given two pixels $p=(x_1,y_1)$ and $p_2(x_2,y_2)$:
For this transform we calculate:
- The distance between each pixel not in the SE mask and the nearest pixel in the mask.
Connected Component Labelling
This is also known as region extraction. The idea is to:
- Group pixels into components based on pixel connectivity.
- All pixels in a connected component share the same pixel intensity.
- This could be $N_4$ or $N_8$.
- Label each pixel with a colour or greyscale.
Two-Pass Equivalence Class Resolution
This is a two-pass algorithm:
- Scan the image (row-wise or column-wise), one pixel at a time:
- When encountering a foreground pixel, look at the previously scanned, neighbour pixels (with 8-connectivity):
- If any of the neighbours have a label assigned, assign the same label to the pixel.
- If neighbouring pixels have more than one labels assigned, pick one arbitrarily.
- Otherwise, assign a new label.
- Every time a label is added, add that label to the equivalence table as a new row.
- If two neighbouring pixels represent the same region, add them to the same row.
- Continue until all pixels are covered.
- Assign new labels for the rows of the equivalence table:
- Scan the image pixel-by-pixel again, new labels to consolidate existing labels.
Shapes
A shape is an image region that can be defined using a set of finite boundary points.
Geometrical Features
The geometry of a region can be characterised in many ways:
- Area
- The number of pixels covered by the region.
- Centroid
- The position of the geometrical centre of the region
- Major/Minor Axis
- The length of the major/minor axis of an ellipse that has the same second moments as the region.
- Eccentricity
- The eccentricity of the ellipse is the ratio of the distance between the foci of the ellipse and its major axis.
- Orientation
- The orientation of the ellipse.
- Euler Number
- The number of holes within the region
- Inscribed Radius
- The radius of the largest cirlce that is contained by the region
- Circumscribed Radius
- The radius of the smallest circle that contains the region.
Some features that are dependent of a regions distribution of intensity are:
- Centre of Mass
- The position of the centre of the region.
- Weighted by the intensities of the pixels.
- Often the centre of mass’s displacement from the centroid is of interest.
- Image Moments (Statistical)
- Mean, variance, skewness.
We can define types of shapes by using correlations between these features.
Morphology is concerned with the shape of structures.
Morphological Erosion
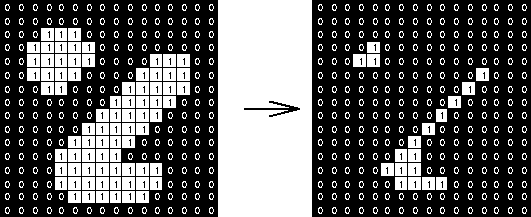
The final image is a subset ($\subseteq$) of the original image.
Allows objects to shrink and separates objects & regions.
It is a pixel-by-pixel operation, sliding the structuring element (SE) at every pixel:
- If the origin of the SE coincides with a 0 (background pixel) of the image:
- There is no change, move the the next pixel.
- If th origin of the SE coincides with 1 (foreground pixel):
- Perform an
AND operation on all the pixels within the SE.
Pixel-by-pixel operations are very slow.
Erosion is expressed by the set operation:
\[A\ominus B\]
where:
- $A$ - The source image.
- $B$ - The structuring element.
This is good for getting rid of salt noise (white spots) on images.
Morphological Dilation
This is the opposite of erosion, allowing objects to expand.
It is a pixel-by-pixel operation, sliding the structuring element (SE) at every pixel:
- If the origin of the SE coincides with a 0 (background pixel) of the image:
- There is no change, move the the next pixel.
- If th origin of the SE coincides with 1 (foreground pixel):
- Perform an
OR operation on all the pixels within the SE.
This results in the maximum output of the local region of the structuring element.
Dilation is expressed by the set operation:
\[A\oplus B\]
This is good for getting rid of pepper noise.
Other Morphological Operations
Morphological Opening
This is erosion followed by dilation with the same structuring element:
\[A\circ B = (A\ominus B)\oplus B\]
This smooths contours and removes noise.
Morphological Closing
Dilation followed by erosion with the smae structuring element:
\[A\bullet B = (A\oplus B)\ominus B\]
Joins nearby connected components together.
We can get the boundary of an object by:
- Eroding with a suitable SE.
- Subtract this form the original image.
\[\beta(A) = A-A\ominus B=A-(A\ominus B)\]
Extraction of connected components can be performed using morphological operation as an iterative procedure.
- Let $x_k$ denote the set of connected foreground pixels at the $k^{\text{th}}$ iteration.
- Start the procedure at one of the connected foreground pixels $x_0$.
- $x_0$ is known as the seed.
- Dilate this pixel: $x_0\oplus B$
-
To stop this dilation becoming connected to pixels which are not part of this component, perform a logical AND with the image:
\[(x_0\oplus B)\cap A\]
- Use the resulting output as the seed for the next iteration.
- Repeat this until no more extractions can be made.
This can be expressed in the following steps:
-
Do for $k={1,\ldots}$:
\[x_k(x_{k-1}\oplus B)\cap A\]
-
Until:
\[x_k=x_{k-1}\]
Region Filling
This closes holes in objects. It consists of the following steps:
-
Set:
\[x_0=1, x_x\oplus B\]
-
Do for $k={1,\ldots}$:
\[x_k=(x_{k-1})\cap \bar A\]
-
Until:
\[x_k = x_{k-1}\]
This searches for images the structuring component in an image. It is given by:
\[A\otimes B=(A\ominus B_1)\cap(\bar A\ominus B_2)\]
Where we have two structuring elements:
\[B_1\cap B_2=\emptyset\]
Skeletonisation
This is the process for reducing foreground regions in a binary image to a skeletal remnant.
Let $A$ be an image and $B$ be a structuring element.
Let $(A\ominus kB)$ denote $k$ successive erosions of $A$ using $B$.
The the skeleton of an image $A$ is:
\[S(A)=\bigcup^K_{k=0}\left\{(A\ominus kB)-(A\ominus kB)\circ B\right\}\]
- $K$ is the maximum number of iterations before the image is eroded to nothing.
Top-Hat
The difference between the image $I$ and the opened version of the image $I$:
\[T(I)=I\hat\circ s=I-I\circ s\]
This returns object of an image that are:
- Smaller than the SE
- Brighter than their surroundings.
This highlights peaks.
Bottom-Hat
The difference between the closed version of the image and the image $I$:
\[B(I) = I\hat\bullet s=I\bullet s-I\]
Returns objects of an image that are:
- Smaller than the SE
- Darker than their surrounding.
This highlights valleys.
Filtering
Filtering is a neighbourhood operation:
- The output pixel is a function of neighbourhood pixels.
Linear Filtering
The output pixel is a linear combination of input pixels.
We use a mask that contains weights to be assigned to each pixel:
- The operation is applies to every pixel by sliding the mask.
- The output pixel is the sum of the input pixels multiplied by the weights in the mask.
Non-Linear Filtering
Anything that is not linear:
- Square mean of neighbourhood pixels.
- Median of neighbourhood pixels.
Mean Filtering
The idea is to take an average of all $N8$ pixels:
- The filter has equal weights across all pixels in the neighbourhood.
Mean filtering is good to remove Gaussian noise.
The original data of the image is modified.
When averaging pixels on the edges of the image, non-existent pixels are treated as 0.
Linear Filtering, Cross-Correlation & Convolution
Linear filtering is the same as cross-correlation of two signals.
Convolution is the same as cross-correlation by the kernel is rotated by 180 degrees.
This is the same as mean but the median of neighbourhood pixels instead of average.
Requires sorting of $N8$ weighted pixel value.
This is good for salt-and-pepper noise and preserves edges.
Gaussian Filtering
The mask is obtained using the following equation:
\[G_\sigma=\frac1{2\pi\sigma^2}e^{-\frac{(x^2+y2)}{2\sigma^2}}\]
we substitute in $(x,y)$ of the mask pixel to find it’s value.
The degree of smoothing is controlled by both the mask size and $\sigma$.
This filter produces a good output for use with edge detection algorithms.
Gain-Offset Correction
This determines the contrast in an image. We may have to re-scale images in a video to ensure all images in a sequence have similar brightness and contrast.
This correction fixes two issues of image sensors:
- Gain - A multiplicative error in the output.
- Offset - An additive error in the output.
Scaling & Equalisation
Scaling and equalisation clips and distorts the raw image data to produce a more appealing image. This can reduce the information in the final image. The following methods can be used:
- Histogram Equalisation - Aims to improve apparent contrast.
- Rescales the intensities so that the intensity distribution is near uniform.
Given an image histogram:
- $r$ is the original grey level (between 0 and $L-1$).
- $s$ is the transformed output grey level (also between 0 and $L-1$).
Contrast Stretching
This method is for enhancing images with little contrast.
Given that the detail is given between $r_a$ and $r_b$:
Given that the detail is given between $r_a$ and $r_b$:
- Set all pixels in the range to a fixed (brighter) value.
Bit-Plane Slicing
Bit plane slicing is used to separate out useful information within an image:
- In an $n$-bit image, each pixel has $n$ bits and there are $n$ planes.
- The MSB contains the majority of the visually significant data.
- The LSB is essentially noise.
Histogram Stretching
For an ideal image, the image histogram is flat. We can perform histogram stretching to spread a peak to fill the histogram:
- Assume that a histogram of a low contrast image ranges from grey value $\check g$ to $\hat g$.
- Assume that we wish to spread this to $[0,G-1]$.
- where $G-1>\hat g-\check g$.
We can do this transform with the following function:
\[g'=\left\lfloor\frac{g-\check g}{\hat g-\check g}G+\frac12\right\rfloor\]
This simple method only stretches the whole histogram. The process of flattening an image histogram is called histogram equalisation.
Always filter noise before using edge detection to improve the results.
Derivative Filters
Derivative (gradient) filters are used to enhance edges as they can highlight sudden changes in an image.
The gradient operator is a vector function of a scalar field:
\[\nabla f=\begin{pmatrix}\frac{\partial f}{\partial x}\\\frac{\partial f}{\partial y}\end{pmatrix}\]
As we don’t have a continuous domain we can use a finite approach:
\[\begin{aligned}
\frac{\partial f}{\partial x}[x,y]&\approx f(x+1,y)-f(x,y)\\
\frac{\partial f}{\partial y}[x,y]&\approx f(x,y+1)-f(x,y)
\end{aligned}\]
gradient of an image $f$ is:
\[\nabla f=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\]
Derivative of Images
Since pixel values represent intensities, gradient points are in the direction of the maximum change in intensity:
-
Change in $x$ direction:
\[\nabla f=\left(\frac{\partial f}{\partial x},0\right)\]
-
Change in $y$ direction:
\[\nabla f=\left(0,\frac{\partial f}{\partial y}\right)\]
-
Change diagonally:
\[\nabla f=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\]
The edge strength is given by the magnitude of the gradient:
\[\left\vert\nabla f\right\vert=\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\]
The direction of the gradient is given by:
\[\theta=\tan^{-1}\left(\frac{\frac{\partial f}{\partial x}}{\frac{\partial f}{\partial y}}\right)\]
Gradient Operators
Edge detection can be completed using small convolution filters, usually two or three pixels square.
Given an image $I$ and a derivate kernel $d$, a pixel value $p$ is computed as a convolution:
\[p=d*h_p(I)\]
Three common gradient operators are:
-
Roberts:
\[\begin{pmatrix}1&0\\0&-1\end{pmatrix}\begin{pmatrix}0&1\\-1&0\end{pmatrix}\]
-
Prewitt:
\[\begin{pmatrix}-1&-1&-1\\0&0&0\\1&1&1\end{pmatrix}\begin{pmatrix}-1&0&1\\-1&0&1\\-1&0&1\end{pmatrix}\]
-
Prewitt:
\[\begin{pmatrix}-1&-2&-1\\0&0&0\\1&2&1\end{pmatrix}\begin{pmatrix}-1&0&1\\-2&0&2\\-1&0&1\end{pmatrix}\]
These operators sum to zero, so a region with no edges gives a zero response.
To use the operators:
- Sum the mask multiplies by the image (element by element) for each operator.
- Take the modulus of both components and add them both together.
Canny Edge Detection
Canny edge detection is good for detecting weak edges. It consists of:
-
Gaussian Blur
We can modify $\sigma$ to change the performance of the edge detection.
- Sobel Operator
-
Calculate Edge Strength (magnitude of Sobel operator)
This is checked to ensure that is a a true edge (local maxima).
-
Calculate the edge angle (arc-tan of the ratio of Sobel components)
This is rounded to 0, 45, 90 and 135 degrees to find the edge direction.
A large $\sigma$ for the Gaussian blur suits wide edges and vice-versa.
Pronounced “Huff”, it is used to detect lines and other geometric shapes.
Any line can be described by an equation in the form:
\[x\cos\theta+y\sin\theta=\rho\]
where $\rho$ and $\theta$ are parameters that specify the line. Any point on the same line has the same values for $\rho$ and $\theta$.
Algorithm for Detecting Straight Lines
- Detect Edges (Canny)
- Map the edges points to Hough Space
- Accumulate the number of points.
- Interpret the accumulator values to interpret lines of infinite length.
This is a computationally intensive task.
Segmentation is the separating of objects from the background. It divides images into regions.
Edges & Regions
Edge enhancement can divide images into regions:
- Each region is bounded by an edge.
A threshold can detect edges in an edge enhanced image.
Edge Linking
Due to noise, edges may be unclear:
- Edges may not be continuous.
- Regions may not be self-contained.
We use edge linking to solve these issues. To link up “loose ends” in an image we can use:
- Linking nearest neighbours.
- Linking all within a given distance.
- Probabilistic linking.
“Snakes”
Snakes is an advanced edge-linking or region extraction algorithm:
- Uses defined edges and a cost-minimisation technique to find regions.
- The cost function is minimised when the edges match the underlying features.
- The optimisation can be done using any standard algorithm.
Thresholding
Some objects are not large enough to generate detectable edges (such as a small house in an image of a large valley).
A simple method for segmentation is to use multiple thresholds:
- To select a certain band of grey levels.
- The pixels in a region will often have a similar intensity.
Variance Growth
A problem with thresholding is with variance in light within an image. An automated method to threshold an image is by using variance growth:
- Images often contain large regions with similar intensities.
- Objects of interest are typically have a different brightness to their background.
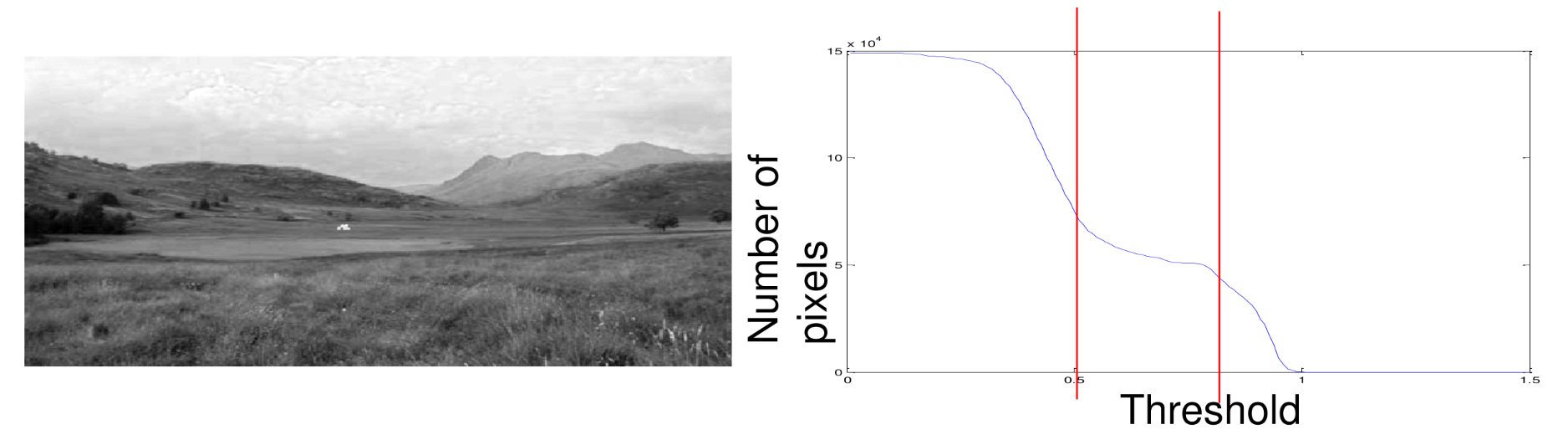
We want to choose a threshold on the flat part of the histogram.
Statistical Texture
We can use a kernel to define the neighbourhood of a pixel. These pixels are connected to the central pixel:
If you take the mean of the kernel:
- Pixels in the same region will tend towards the central pixel.
Watershed Algorithm
- Represent the image as a surface (with height defined by pixel intensity).
- Applying a thresholding “flood-fill”:
- Link connected pixels to form the background.
- Repeat this to form several regions as layers.
Colour Segmentation
We can start by representing the image in HSL:
- We can then threshold on the hue or saturation channels to find the object.
Motion Segmentation
We can separate moving objects from stationary backgrounds:
- Take the difference between the two images to clearly identify the object.
We can remove small camera motions and noise by using noise filtering on the output.
Region Labelling
After segmentation, region labelling is required. The result of image segmentation is a binary image with the foreground represented by ones.
Typically there will be a large number of foreground regions, this contains:
To distinguish the regions we label connected foreground pixels. We use:
- Connected Component Labelling
- Extracting Connected Components
Noise in Segmentation
By knowing the type of noise (white, Gaussian, photon) we can use an appropriate model to remove it effectively.
Blur is also a form of noise. To deal with this we change change our blur model to account for blur caused by the sensor.
Lossless Compression
Relies on probabilistic theory:
- Events that are less likely will contain more information.
A measure of average information is entropy also known as Shannon’s Information Measure:
\[H(x)=\sum_{i\in x}p(i)\log_2\left(\frac1{p(i)}\right)\]
where:
- $x$ is a probabilistic experiment.
- $x_i$ are all the possible outcomes
The base of the logarithm is the unit of information (base 2 means that it is measured in bits).
Entropy of an Image
The entropy $E$ of an $N\times N$ image is:
\[E=-\sum^{L-1}_{i=0}p_i\log_2(p_i)\]
where:
- $p_i$ is the probability of the $i^\text{th}$ greylevel.
- $L$ is the total number of greylevels.
additionally:
\[0\leq E\leq \log_2L\]
The average number of bits per pixel in a coder is:
\[\hat L=\sum^{L-1}_{i=0}l_ip_i\]
where:
- $p_i$ the probability of the $i^\text{th}$ greylevel.
- $l_i$ length in bits of the code for the $i^\text{th}$ greylevel.
Image Entropy Example
Consider an image uses 3 bpp and the histogram is flat across the domain:
- As there are 3bbp there are 8 greylevels ($L=8$).
- Flat histogram means that the number of pixels at each greylevel are the same ($p_i\frac18$).
\[\begin{aligned}
E&=-\sum^{L-1}_{i=0}p_i\log_2(p_i)\\
E&=-\sum^{7}_{i=0}\frac18\log_2(\frac18)\\
E&=3
\end{aligned}\]
This means that there is no code that will provide better coding that what is used by default. An image with a flat histogram has the highest entropy.
Huffman Coding
This is a type of coding that encodes frequent symbols as short strings of bits and infrequent symbols as longer bit strings.
- This is a minimum length code (it will generate close to the theoretical minimum).
- It generates variable length code.
Method:
- Sort the symbols in decreasing order of probability.
- Combine the smallest two by addition.
- Replace the two elements with a single combined element.
- Goto step 2 until only two probabilities are left.
- Work backwards along the tree and generate the code by alternating 0 and 1.
Huffman Coding Example
Consider a 10x10 image that uses 2bpp with the following histogram:
| Greylevel |
Count |
| 0 |
20 |
| 1 |
30 |
| 2 |
10 |
| 3 |
40 |
-
Find the probability of each level:
| Greylevel |
Probability |
| 0 |
.2 |
| 1 |
.3 |
| 2 |
.1 |
| 3 |
.4 |
-
Sort in descending order:
| Greylevel |
Probability |
| 3 |
.4 |
| 1 |
.3 |
| 0 |
.2 |
| 2 |
.1 |
-
Add the bottom two rows:
Original
Greylevel |
Probability |
Reduction 1 |
Reduction 2 |
Sort 2 |
| 3 |
.4 |
.4 |
.4 |
.6 |
| 1 |
.3 |
.3 |
.6 |
.4 |
| 0 |
.2 |
.3 |
|
|
| 2 |
.1 |
|
|
|
Sort between each iteration.
This gives the following Huffman tree:
graph TD
a(( )) -->|0| b(("g3 (00)"))
a -->|1| c(("g1 (1)"))
b -->|0| d(("g0 (010)"))
b -->|1| e(("g2 (011)"))
Coding Efficiency
Coding efficiency is defined as the ratio of entropy to the average number of bits per symbol.
For images we write this as:
\[\eta =\frac E{\hat L}=\frac{-\sum p_i\log_2 pi}{\sum l_ip_i}\]
Bit Plane Decomposition
We can make use of bit plane decomposition to compress an image. We can then use compression techniques on each plane, to take advantage of contiguous blocks in the most significant bits.
Constant Area Coding
Break the bit planes up into smaller sections of $n_1\times n_2$ pixels.
Each subsection can be encoded:
- 0 if it is white
- 10 if it is black
- 11 if it mixed black and white (followed by the bits used in the block).
Run Length Encoding
In a binary image we can encode a line with runs of zeros first.
A line of:
\[11111000011\]
would be encoded as:
There are zero 0s to start so we start with a zero.
Lossy Compression
JPEG
JPEG uses one of the following coding schemes:
- Lossy baseline coding:
- Based on discrete coding transform (DCT).
- Extended coding for greater compression.
- Lossless independent coding.
Lossy Baseline Coding (DCT)
- Pre-processing
- Convert the image to YCbCr.
- Partition the image into 8x8 tiles.
- Centre the intensity values about 0 (subtract 128 from each pixel).
- Transformation
- Apply DCT to the image tile by tile.
- The pushes high-intensity values to the top left corner.
- The top-left is the DC component (average value of the pixels).
- The bottom-right corner is the AC component (has the highest frequency).
- Quantisation
-
Round elements towards zero (like floor).
This removes high frequency components from the image and provides the lossy compression component.
- Encoding
- Reorganise the quantised DCT coefficients into a vector.
- Oder the coefficients in a zig-zag order.
- Apply Huffman coding.