Methods of Proof
- Counter Example Method
- Prove that a statement is false by use of a counter-statement.
- Universal Proof
- Applies to all integers e.g. odd if $a=2k+1$
Example
\((a+b)^2=a^2+b^2\)
Holds for:
- Some integers
- All integers
- No integers
The answer is that it holds for some integers as when $a=0,\ b=0$. \((0+0)^2=0^2+0^2\) This also follows for $a\neq0,\ b=0$.
The two proofs I gave as answers to the question count for both a counter example proof and a universal proof.
Example of Proof by Contradiction
Suppose for a proof by contradiction that $P_n$ is the largest prime number. Therefore, $P_1\ldots P_n$ are all the primes.
Consider $P=P_1\times P_2\ldots P_n+1$
Case 1: $P_p$ is prime
Case 2: $P_p$ not prime. Then $P$ must have prime member.
This is following the questions from the tutorial for week 1.
The tutorial leader’s email is: p.austin@liverpool.ac.uk
Notion of Proof
Types of Numbers
- Natural numbers $\mathbb{N}$ are whole numbers that start from 0.
- Integers are whole numbers including negatives.
- Rational numbers are any number that can be represented as fractions without a denominator of 0.
- Real numbers are any decimal number that can be presented on a number line. E.g. $\pi$
Proofs
A mathematical proof is a carefully reasoned argument to convince a sceptical listener that a statement is true.
Properties of Odd and Even Numbers
An even number $m$ is in the form $m = 2k$ where $k$ is an integer.
An odd number $n$ is in the form $n= 2l+1$ where $l$ is an integer.
Notation
- The symbol $\exists$ means exists.
- The symbol $\Leftrightarrow$ means if and only if.
- The symbol $\forall$ means for all.
Some definitions written in notation may look like:
Proving Existential Statements
An existential statement is a statement in the form:
\(\exists x\ Q(x)\)
This means that there exists a value to which the function $Q(x)$ holds true. This may be under additional parameters.
The easiest way to prove this is to find an $x$ that makes the function $Q(x)$ true. Not all can be proved this way.
Examples
- $\exists$ an even integer $n$ that can be written in two ways as a sum of two prime numbers.
\(10=5+5=7+3\)
- There $\exists$ integers $m$ and $n$ such that $m>1$, $n>1$ and $\frac{1}{m} + \frac{1}{n}$ is an integer.
\(m=n=2\)
Giving an example is a suitable proof.
Proving Universal Statements
Generally proofs will require you to answer a universal statement rather than an existential one. an existential statement is of the form:
\(\forall x \text{ if } P(x) \text{ then } Q(x)\)
This means that for all of $x$ if one function is applied to $x$ another function in $x$ also holds true. For example:
If $a$ and $b$ are integers then $6a^2b$ is even.
In this statement the “$a$ and $b$ are integers” count for $P(x)$ and “$6a^2b$ is even” counts for $Q(x)$.
$6a^2b$
$2(3a^2b)$
By halving you are proving that the answer is even as it is a multiple of two.
Proof by Exhaustion
For theorems examining a relatively small number of examples you can test each value to see if the statement holds true. That is proof by exhaustion.
Example
- Prove that $(n+1)^3 \geq 3^n$ if $n$ is a positive number.
As this theorem has such a small scope then each value can be tested to see if it is correct.
Generalising from the Generic Particular
This method allows for using algebra and known rules to prove a statement generally.
Method
- Express the statement to be provided in the form $\forall x,\text{ if } P(x) \text{ then } Q(x)$
- Start the proof by supposing $x$ is a particular by arbitrarily chosen element for which the hypothesis $P(x)$ is true.
- Show that the conclusion $Q(x)$ is true by using definitions, previously established results, and the rules for logical inference.
graph LR
Definitions --> A[Conjecture]
B[Known Facts] --> A
This method brings together definitions and facts into a conjecture.
Example
Prove that the sum of any two even integers is even.
- (Assume that/Suppose that) $m$ and $n$ are particular but arbitrarily chosen even integers.
- As we assumed that $m$ is an even integer, $m = 2k$ for some integer $k$.
- Likewise $n$ is an even integer, $n = 2l$, for some integer $l$
- We cannot use the same letter again as $k$ has already been used
- Then $m+n=2k+2l=2(k+l)$, which is even as $k+l$ is an integer.
The final step is called the conjecture as is aided by the previous steps to explain why the conjecture holds true.
Disproving Universal Statement by Counterexample
To disprove a statement means to show that it is false. For example, for a statement such as:
\(\forall x \text{ if } P(x) \text{ then } Q(x)\)
You are saying that the opposite is true:
\(\exists x \text{ such that } P(x) \text{ and not } Q(x)\)
This means that you must give at least one example that disproves the universal statement.
Example
Is it true that for every positive integer $n,n^2\geq 2n$?
No as for $n=1,\ n^2 = 1$ and $2n=2$ which is greater than $n^2$
You can correct this by stipulating that for ever integer greater than one the statement holds true.
More Examples of Direct Proof
- $\forall\ n$ if $n$ is an integer then $n$ is rational.
- Proof: Suppose that $n$ is a particular but arbitrarily chosen integer.
- $n=\frac{n}{1}$
- By definition of a rational number $\frac{n}{1}$ is rational.
- $\forall\ r$ and $s$, if $r,s$ are rational then $r+s$ is rational.
- Proof: Suppose that $r$ and $s$ are particular but arbitrarily chosen rational numbers.
- As $r$ is rational $r=\frac{l}{m}$ where $l,m$ are integers, $m\neq 0$.
- As $s$ is rational $s=\frac{i}{k}$ where $i,k$ are integers, $k\neq 0$.
- Then $r+s = \frac{l}{m} + \frac{i}{k} = \frac{lk+mi}{mk}$
- As $m\neq 0, k\neq 0$ we derive that $mk\neq 0$
- As $lk+mi,mk$ are integers, $mk\neq 0$ we conclude that $r+s$ is a rational number.
Proof by Cases
For proofs that have multiple cases then you can prove that the statement holds for each case to give a universal proof.
Example 1
For all integers $n,\ n^2 + n$ is even.
Proof
Case 1: $n$ is even
- Then $n=2k$, for some integer $k$
- $(2k)^2+2k=4k^2+2k=2(2k^2+k)$
- By definition of even, $n^2 + n$ is even.
Case 2: $n$ is odd
- Then $n=2k+1$, for some integer $k$.
- $(2k+1)^2+(2k+1)=4k^2+6k+2=$ $2(2k^2+3k+1)$
- By definition of even, $n^2 + n$ is even.
As both cases (which are all cases) conclude the same thing then the statement is considered proved.
Example 2
Prove that the product of any two consecutive integers is even.
Rewording
$\forall\ n$ if $n$ is an integer then $n(n+1)$ is even.
Proof
Consider that $n$ is a particular but arbitrarily chosen integer. We proof the statement by a consideration of cases.
Case 1: $n$ is even.
Case 2: $n$ is odd.
- Then $n=2k+1$, for some integer $k$.
- So $n(n+1)$ $=(2k+1)((2k+1)+1)$ $= (2k+1)(2k+2)$ $= 2(2k+1)(k+1)$.
Indirect proofs
In a direct proof you start with the hypothesis and make deductions until you reach the conclusion.
For an indirect proof you can make use of contradictions to prove statements logically. An example may be in a Sudoku puzzle where you prove which number goes in a square based on the fact that it can’t be any other number.
Proof by Contradiction
If it is not the case that it is not true. It must be the case that it is true.
graph LR
D[Definitions] --> C[Contradiction]
K[Known Facts] --> C
N[Negated Conjecture] --> C
Examples
-
Show that there is not greatest integer.
Proof: Suppose for a proof by contradiction that the conjecture is not true.
Then there is an integer larger than any other integer.
Let $N$ be such an integer.
So $N>N+1$ and therefore 0>1, which is a contradiction.
Therefore, our assumption that the conjecture is not true is false. So there is no greatest integer.
-
No integer can be both even and odd.
Proof: Suppose for a proof by contradiction that this conjecture is not true.
Then there exists an integer $N$ which is both even and odd.
By definition of even, $n=2l$, for some integer $l$.
By definition of odd, $n=2k+1$, for some integer $k$.
$2l=n=2k+1$. So $2l=2k+1$. Then $2l-2k=1$. Then $2(k-l) = 1$.
Then 1 must be even, which is a contradiction.
Therefore, we can conclude that no integer can be both even and odd.
Proof by Contraposition
To prove
\(\forall \text{ if } P(x) \text{ then } Q(x)\)
it suffices to prove
\(\forall \text{ if not } P(x) \text{ then not } Q(x)\)
Example
- For all integers $m$ if $m^2$ is even then $m$ is even.
- For all integers $m$ if $m$ is not even then $m^2$ is not even.
This can be re-written as:
- For all integers $m$ if $m$ is odd then $m^2$ is odd.
This can then be taken into a direct proof however it may make more sense to prove by contradiction instead of contraposition and it is the preferred method at this time.
Two Classic Results
These are classical proofs as they we’re proven by the Ancient Greeks. They are both proofs by contradiction.
Use proof by contradiction to show that there is no greatest prime number.
- 2, as the smallest prime number, is known as $P_1$. All following prime numbers are numbered sequentially.
- For each prime number that is identified any multiples are removed from the endless list of integers.
- This is continued for $P_2=3$ where all multiples of 3 are removed.
How do we know that at some point in the list all numbers are eliminated?
Proof
Assume for a proof by contradiction that there is a greatest prime number $P_n$.
Then $P_1, P_2, \ldots , P_n$ are all prime numbers.
Consider $P=P_1\times P_2\times \ldots \times P_{n+1}$
Consider cases:
Case 1
$P=P_1\times P_2\times \ldots \times P_{n+1}$ is prime. As $P>P_n$ we derive a contradiction.
Case 2
$P$ is not a prime. Then $P$ has a divisor (all numbers can be expressed as a product of primes).
Then $P$ has a prime factor.
So one of $P_1, P_2, \ldots , P_n$ must divide $P$. This number can be called $P_i$.
\[\begin{aligned}
P&=P_i\times Q,\ Q\neq 1\\
P_1\times\ldots P_{n+1}&=P_i\times Q\\
P_1\times\ldots P_{i-1} \times P_i \times P_{i+1} \times\ldots P_{n+1}&=P_i\times Q\\
P_i \times Q - P_i (P_1 \times\ldots\times P_{i-1} \times P_{i+1} \times P_n)&=1\\
P_i(Q-P_1 \times\ldots\times P_{i-1} \times P_{i+1} \times\ldots\times P_n) &= 1
\end{aligned}\]
This is a contradiction as one is not a product of two distinct integers.
As a result the statement that there is no greatest prime number.
Prove that $\sqrt{2}$ is not a Rational Number
Assume for a proof by contradiction that $\sqrt{2}$ is rational.
Then there exist integers $m,n$ such that $\sqrt{2}=\frac{m}{n}, n\neq 0, \frac{m}{n}$ is not reducible.
Then $(\sqrt{2})^2=(\frac{m}{n})^2$. Then $2=\frac{m^2}{n^2}$.
Then $2n^2=m^2$. So $m^2$ is even.
We already know that $m$ must be even.
By definition of even $m=2k$ for some integer $k$.
$2n^2=m^2, m=2k$
$2m^2=(2k)^2$. Then $2n^2=4k^2$. Then $n^2=2k^2$, so $n^2$ is even.
Then $n$ is even.
So we derive a contradiction as n and m have a common factor of $2$. As it is reducible it doesn’t follow the rule.
Indirect Proof of Existential Statements
Prove that there exist irrational numbers $q$ and $r$ such that $q^r$ is rational.
Consider Cases:
Case 1
If $\sqrt{2}^{\sqrt{2}}$ is a rational number then we are done and $q=\sqrt2, r=\sqrt2$.
Case 2
$\sqrt{2}^{\sqrt{2}}$ is not rational. Then:
$q=\sqrt{2}^{\sqrt{2}}, r=\sqrt2$
$q^r = (\sqrt2^{\sqrt2})^{\sqrt2}=\sqrt2^{\sqrt2\sqrt2}=\sqrt2^2=2$
- They are used to check conjectures about outcomes of processes that occur repeatedly and according to definite patterns.
- In general, mathematical induction is a method for proving that a property defined for integers $n$ is true for all values of $n$ that are greater than or equal to come initial integer.
Generic Particular v.s. Induction for Universal Statements
Generalisation from the generic particular:
“Suppose that $x$ is a particular but arbitrarily chosen…” “…property holds for this $x$…” “…then the property holds for all $x$”
This argument states that as we have chosen an arbitrary value from a set then the argument will hold for all numbers within the same set.
Induction
We apply a process to all the values in a set. This process is carried on until an arbitrary value is reached.
- Prove that the property holds for some initial value (e.g. $n=0$).
- Prove that if the property hold for $n=m$ (for any natural number $m$) then it holds for $n=m+1$.
Example
For a set of dominoes the following process can be applied:
For a domino at position $i$, when it is pushed the domino at position $i+1$ will fall sequentially.
The conclusion can be that all of the dominoes will fall.
Typical Structure
We prove the statement by mathematical induction on $n$.
Base Case
Show that the property hold for some initial value (e.g. $n=0$).
Inductive Step
Assume that the property holds for $n=m$. Show that is hold for $n=m+1$.
Conclusion
You can now conclude that the property holds for every natural number $n$.
Carl Friedrich Gauss
\(1+\ldots+100=5050\)
If you split the number line in the middle the sum of every column is 101. With 50 columns the answer is 5050.
For every natural number $n$,
\(0+1+\ldots+n=\frac{n(n+1)}{2}\)
Proof
Base Case
$n=0$
$0 = \frac{0(0+1)}{2} = 0$
Inductive Step
Suppose that for $n=m$ the property holds.
Then:
\[0+1+\ldots+m=\frac{m(m+1)}{2}\]
Consider the statement for $n=m+1$.
$0+1+2+\ldots+m+(m+1)$.
By induction hypothesis, $0+1+\ldots+m=\frac{m(m+1)}{2}$
So,
\[\begin{aligned}
0+1+\ldots+m+(m+1)&=\frac{m(m+1)}{2}+(m+1)\\
&=\frac{m(m+1)}{2}+\frac{2(m+1)}{2}\\
&=\frac{m(m+1)+2(m+1)}{2}\\
&=\frac{(m+1)(m+2)}{2}\\
&=\frac{(m+1)((m+1)+1)}{2}\\
&=\frac{n(n+1)}{2}
\end{aligned}\]
This shows that for any sequential number the fraction simplifies to the statement, thus proving that it holds for any number.
Using induction to show that a program is correct.
Example on a Recursive Function that Generates Factorials
Proof
By mathematical induction on $n$.
Base Case $n=1$
\(g(1)=1=1!\)
Inductive Step
Suppose that for some $n=m, g(n)=n!$
Consider $n=m+1$
$g(m+1)$ the code returns $g(m)\times(m+1)$
By induction hypothesis, $g(m)=m!$
So:
\(g(m)\times(m+1)=m!\times(m+1)=(m+1)!\)
For a normal case of mathematical induction you can prove that a statement holds for all numbers from a particular start point.
It uses a base case so show that it holds for an individual number and an induction rule that proves that it holds for all numbers following.
- Prove that the property holds for the natural number $n=0$
- Prove that if the property holds for $n=0,1,\ldots,m$ (and not just for m) then it holds for $n=m+1$.
Can also be used to prove a property for all integers greater than or equal to some particular natural number $b$.
Example 1
Every natural number $n \geq 2$, is a prime or product of primes.
Base Case
Take $n=2$
Then $n$ is a prime number.
Inductive Step
Assume that the property holds for $n=m$ so every number $i$ such that $2\leq i\leq m$ is a prime or a product of primes.
Now consider $n=m+1$.
We proceed by considering cases.
Case 1
$m+1$ is prime.
There is nothing to prove.
Case 2
$m+1$ is not prime.
So $m+1=k\times l$, where $k\neq1,\ k\neq m+1$ and $l\neq 1,\ l\neq\ m+1$
So $k\geq2,\ l\geq2,\ k\leq m,\ l \leq m$
So $k=P_1\ldots P_n,\ l=Q_1\ldots Q_m$. Then $k\times l$ is a product of primes.
Example 2
For any integer $n\geq1$, if $x_1,x_2,\ldots,x_n$ are $n$ numbers, then no matter how the parentheses are inserted into their product, the number of multiplications used to compute the products is $n-1$.
As the number are all individual you can’t use tricks like using already computed values to speed up the computation.
Base Case
\(X_1 \text{ for } n=1,\ n-1=0\)
Induction Step
Suppose that no matter how I put parentheses on a sequence of $i$ elements, where $1\leq i\leq m$, I need $m-1$ multiplications.
Consider, where $1\leq l \leq m$:
\[\underbrace{\underbrace{(x_1\times\ldots)}_{l}\times\underbrace{(\ldots\times x_{m+1})}_{m+1-l}}_{m+1}\]
By induction hypothesis:
\[\require{cancel}\cancel{l}-1+m+1-\cancel{l}-\cancel{1}+\cancel{1}=(m+1)-1\]
This proves that the property holds for the next value to infinitude. $\square$
Definitions of Supplementary Statements
Conjectures are built on other conjectures. They can be subdivided into the following parts:
- Theorem
- A very important true statement.
- Proposition
- A less important by still interesting statement.
- Lemma
- A true statement used to prove other statements.
- Corollary
- A simple consequence of a theorem or a proposition.
Finishing Proofs
At some point in a proof, you’ll have established all the essential facts you need. Resist the temptation to quit and leave the reader to draw the “obvious” conclusion. Instead, tie everything together yourself and explain why the original claim follows.
In addition, at the end of a proof use the Latin phrase, “$_\text{QED}$” or $\square$ to show that you have finished the proof.
Notation for Sets
A set is a collection of objects, called the elements of the set.
We have written down the element of each set and contained them between the braces $\{\}$.
Repetitions and orderings don’t matter in sets hence $\{7,5,3\}$ is the same as $\{5,3,3,3,7\}$.
We write $a\in A$ to denote that the object $a$ is an element of the set $a$: \(7\in\\{7,5,3\\},4\notin\\{7,5,3\\}\)
The order of elements does not matter.
Repetitions don’t count.
For a large set, especially an infinite set, we cannot write down all the elements. We use a predicate $P$ instead.
\(A=\{x\in S\vert P(x)\)
denotes the set of objects $x$ from $S$ fro which the predicate $P(x)$ is true.
Example
Let:
\(A = \{1,3,5,7,\ldots\}\)
Then:
\(A=\{x\in \mathbb{Z} \vert x \text{ is odd}\}\)
More Examples
Find simpler descriptions of the following sets by listing their elements. (The set $A$ is written properly however $B$ and $C$ are written informally.
-
$A=\{x\in\mathbb{z}\vert x^2+4x=12\}$
$\{2,-6\}$
-
$B=\{n^2\vert n \text{ is an integer}\}$
$\{0,1,4,9,16,25,\ldots\}$
$B=\{m\in\mathbb{Z}\vert m=n^2$$ \text{ for some integer } n\}$
-
$C=\{x\vert x \text{ a day of the week,}$$\text{ not containing “u”}\}$
$\{\text{Monday, Wednesday, Friday}\}$
Important Sets
The empty set had no elements. It is written as $\emptyset$ or as $\{\}$.
Here are some other sets:
- $\mathbb{N}=\{0,1,2,3,\ldots\}$ The natural numbers.
- $\mathbb{Z}=\{\ldots,-2,-1,0,1,2,\ldots\}$ The integers.
- $\mathbb{Z^+}=\{1,2,3,\ldots\}$ The positive integers.
- $\mathbb{Q}=\{\frac{x}{y}\vert x \in\mathbb{Z},y\in\mathbb{Z},y\neq0\}$ The rationals.
- $\mathbb{R}$ Real numbers.
- $[a,b]=\{x\in\mathbb{R}\vert a\leq x \leq b\}$ The set of real numbers between $a$ and $b$ inclusive.
Computer Representation of Sets
Only finite sets can represented.
- Number of elements not fixed.
- All elements of $A$ are drawn from some ordered sequence $S=\langle s_1,\ldots,s_n\rangle$. The characteristic vector of $A$ is the sequence $[b_1,\ldots,b_n]$ where:
\(b_i=
\begin{cases}
1 & \text{if}\ S_i\in A \\
0 & \text{if}\ S_i\notin A
\end{cases}\)
- Sequences of zeros and ones of length $n$ are called bit strings of length $n$. These are also known as bit vectors or bit arrays.
Examples
Let $S\langle 1,2,3,4,5\rangle, A = \{1,3,5\}$ and $B=\{3,4\}$
- Characteristic vectors show how sets relate to sequences. The $1$ shows that the value is in the set.
- The characteristic vector of $A$ is $[1,0,1,0,1]$.
- The characteristic vector of $B$ is $[0,0,1,1,0]$.
- You would answer a question in the opposite direction like so:
- The set characterised by $[1,1,1,0,1]$ is $\{1,2,3,5\}$.
- The set characterised by $[1,1,1,1,1]$ is $\{1,2,3,4,5\}$.
- The set characterised by $[0,0,0,0,0]$ is $\emptyset$.
Subsets
A set $B$ is called a subset of a set $A$ if every element of $B$ is an element of $A$. This is denoted by $B\subseteq A$.
Examples
\(\begin{aligned}
\{3,4,5\}&\subseteq\{1,5,4,2,1,3\}\\
\{3,3,5\}&\subseteq\{3,5\}\\
\{5,3\}&\subseteq\{3,5\}
\end{aligned}\)
graph TB
subgraph A
B(B)
end
Venn diagram of $B$ subset $A$.
Therefore, $\forall$ sets $A$, $A\subseteq A$
Furthermore, $\emptyset\subseteq A$ is always true. This is as the empty set is always a subset of any other set including the empty set itself.
Subsets in Python
In programming languages such as python you can save on writing out a function to fund whether a set is a subset of another set. To do this you can use the < symbol in place of the $\subseteq$ symbol:
Where n and m are both sets.
Subsets and Bit Vectors Example
Let $S=\langle1,2,3,4,5\rangle,A=\{1,3,5\}$ and $B=\{3,4\}$.
-
Is $A\subseteq B$?
$x_a=[1,0,1,0,1]$
$x_b=[0,0,1,1,0]$
Therefore $A\nsubseteq B$. As you can see from the aligned bits. Not all the bits present in $x_b$ are present in $x_a$.
-
Is the set $C$, represented by $[1,0,0,0,1]$, a subset of the set $D$, represented by $[1,1,0,0,1]$?
$C\subseteq D$ as all bits present in the bit vector of $C$ are also present in the bit vector of $D$.
Equality
As covered before a set $A$ is called equal to a set $B$ if $A\subseteq B$ and $B\subseteq A$. This is denoted by $A=B$.
This is to say that if two sets are subsets of each other then they are equal.
Confirming Equality
Let $S=\langle1,2,3,4,5\rangle,A=\{1,3,5\}$ and $B=\{3,4\}$.
Is $A=B$?
$x_a=[1,0,1,0,1]$
$x_b=[0,0,1,1,0]$
Therefore $A\neq B$ as the bit vectors do not match.
Union
The union of two sets $A$ and $B$ is the set:
\(A\cup B = \{x\vert x\in A\ \text{or} \in B\}\)
This is the same as logical OR ($+$)
Example
Suppose
\(A=\{4,7,8\},\ B=\{4,9,10\}\)
Then
\(A\cup B = \{4,7,8,9,10\}\)
In bit vectors you just perform a logical OR on both of the bit vectors. The result of the OR is the bit vector of the result of the union.
Intersection
The intersection of two sets $A$ and $B$ is the set:
\(A\cap B = \{x\vert x\in A\ \text{and}\ x\in B\}\)
This is the same as logical AND.
Example
Suppose
\(A=\{4,7,8\},\ B=\{4,9,10\}\)
Then
\(A\cap B = \{4\}\)
In bit vectors the result of the intersection is the same as a logical AND on the bit vectors.
Relative Complement
The relative complement of a set $B$ to a set $A$ is the set:
\(A-B=\{x\vert x\in A\ \text{and}\ x\notin B\}\)
This is the same as XOR ($\oplus$)
This is also sometimes called the set difference.
Example
Suppose
\(A=\{4,7,8\},\ B=\{4,9,10\}\)
Then
\(A - B = \{7,8\}\)
In bit vectors perform an XOR on both of the bit vectors to get the result.
Complement
When we are dealing with subsets of some large set $U$, then we call $U$ the universal set fro the problem in question.
The complement of a set $A$ is the set:
\(\sim A=\{x\vert x\notin A\}=U-A\)
This is the same as a binary NOT $\neg$.
Example
Let
\(S=\langle1,2,3,4,5\rangle,\ A=\{1,3,5\}\)
Then
\(\sim A = \{2,4\}\)
The Symmetric Difference
The symmetric difference of two sets $A$ and $B$ is the set:
\(\begin{aligned}
A\Delta B=&\{x\vert (x\in A\ \text{and}\ x \notin B)\ \text{or}\\
&(x\notin A\ \text{and}\ x \notin B)\}
\end{aligned}j\)
This is the same as the logical operator NAND.
Example
Suppose
\(A=\{4,7,8\},\ B=\{4,9,10\}\)
Then
\(A - B = \{7,8,9,10\}\)
In bit vectors perform an NAND on both of the bit vectors to get the result.
Proving the Identity of $A\Delta B=(A\cup B)-(A\cap B)$
Proof
Suppose that $x$ is a particular but arbitrarily chosen element. Consider all cases of this element:
Case 1
$x\notin A,\ x\notin B$. By definition of $\Delta,\ x\notin A\Delta B$.
By definition of $\cup,\ x\notin A\cup B$.
Hence $(A\cup B)-(A\cap B)$.
Case 2
$x\in A,\ x\notin B$. By definition of $\Delta,\ x\in A\Delta B$
By definition of $\cup,\ x\in A\cup B$ as $x\in A$.
As $x\notin B,\ x\notin A\cap B$.
So $x\in(A\cup B)-(A\cap B)$.
Case 3
$x\notin A,\ x\in B$. This case is symmetric to case 2.
Case 4
$x\in A,\ x\in B$. By definition of $\Delta,\ x\notin A\Delta B$.
As $x\in A$, by definition of $\cup,\ x\in A\cup B$.
As $x\in A,\ x\in B,\ x\in A\cap B$.
So $x\notin (A\cup B)-(A\cap B)$.
By the generalisation from the generic particular principle, the identity holds.
(As both sides are equal for all cases the identity must be valid.)
Suppose that $A,B,C,U$ are sets with $A \subseteq U, B \subseteq U, C \subseteq U$.
Commutative Laws
These laws say that is doesn’t matter in which order the operation takes place.
- $A\cup B = B \cup A$
- $A\cap B = B \cap A$
Associative Laws
These laws say that is doesn’t matter where you put brackets around an operation
- $A\cup(B\cup C)=(A\cup B) \cup C$
- $A \cap(B \cap C) = ( A \cap B) \cap C$
Distributive Laws
This is how the properties of union and intersect propagate between one another. This applies to expanding brackets with mixed signs.
- $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$
- $A\cup(B\cap C)=(A\cup B)\cap(A\cup C)$
Identity Laws
The following sets only apply if there is a universe set or context which the sets are within.
If you join the empty set with anything you get what you joined it with. If you take the intersect of anything and the universe $U$ then you get the thing you intersected it with.
- $A\cup \emptyset = A$
- $A\cap U = A$
Complement Laws
If you take a set and it’s complement (¬) then you get the universe set $U$. The intersect of a set and its complement is the empty set.
- $A\cup\sim A = U$
- $A\cap\sim A=\emptyset$
Double Complement Law
Idempotent Laws
- $A \cup A = A$
- $A \cap A = A$
Universal Bound Laws
- $A\cup U = U$
- $A\cap \emptyset = \emptyset$
De Morgan’s Law
The complement of a union is the intersection of complements.
- $\sim(A\cup B) = \sim A\cap\sim B$
- $\sim(A\cap B) = \sim A\cup\sim B$
Absorption Laws
This is a result of the expansion of brackets.
- $A\cup(A\cap B) = A$
- $A\cap(A\cup B) = A$
Complement of $U$ and $\emptyset$
- $\sim U = \emptyset$
- $\sim \emptyset = U$
Set Difference Law
Disclaimer and Proofs
As none of the above are axioms then you have to reference them if you use them in a proof.
Example 1
$A=\{1,2,7,8,9\}, B=\{x\in A\vert x \text{ is odd}\}$
Where:
$C=A-B=A\cap B$
Therefore:
$B=\{1,7,9\}$
$C=\{2,8\} = \{x\in A \vert x \notin B\}$
Proving Identities
To prove an identity you would consider the sections of a Venn diagram and consider each of the four cases. These cover all of the locations in the Venn diagram.
For the following questions:
- $\emptyset \in\{\text{Leeds, Liverpool}\}$
- $\emptyset \subseteq\{\text{Leeds, Liverpool}\}$
- $\emptyset = \{\}$
- False as they are different types.
The cardinality of a set is the number of elements in the set. The notation for this is $\vert A\vert$ where $A$ is a set to be counted.
Power Set and Bit Vectors
We use the correspondence between bit vectors and subsets: $\left\vert \textit{Pow}(A)\right\vert$ is the number of bit vectors of length $n$.
\[A\ s.t \left\vert A \right\vert = n,\ S_n = \langle\ldots\rangle\]
\[B \subseteq A \rightarrow X_b = \underbrace{\left[\frac{0}{1},\ldots,\frac{0}{1}\right]}_n\]
A bit vector of the set $C$ is represented by the vector $X_C$:
\[X_c=\left[\ldots\right] \rightarrow C\]
This means that provided you know the set you and reconstruct a subset from the bit vector of that subset.
The Number of $n$-bit vectors in $2^n$
We prove the statement by induction
Base Case:
$n=1$
There are two bit vectors of length 1:
$\left[0\right], \left[1\right]$
$2^1=2$
Inductive Step:
Assume that the property holds for $n=m$, so the number of $m$-bit vectors is $2^m$. Now consider the set $B$ of all $(m+1)$-bit vectors. We must show that $\left\vert B\right\vert =2^{m+1}$.
We know that all elements of $B$ are bit vectors of length $m+1$:
\[\underbrace{\left[\hspace{0.5cm},\right]}_{m+1}\in B\]
The first elements apart from the last one are put in a new bit vector:
\[\underbrace{\left[\ldots\right]}_m\]
Given any bit vector there are only two ways of filling in the last value, with a 0 or a 1. As there are two ways of extending a bit vector then you times the bit vector by two.
\[\left\vert B \right\vert = 2 \times 2^m = 2^{m+1}\]
Computing the Cardinality of a Union of Two Sets
If $A$ and $B$ are sets then:
\[\left\vert A \cup B \right\vert = \left\vert A \right\vert + \left\vert B \right\vert - \left\vert A\cap B \right\vert\]
Example
Suppose there are 100 third-year students. 40 of them take the module “Sequential Algorithms” and 80 of them take the module “Multi-Agent Systems”. 25 of them took both modules. How many students took neither modules?
\[\begin{aligned}
S&=\{s\in \text{Student} \vert s \text{ takes Seq. Alg.}\}\\
M&=\{s\in \text{Student} \vert s \text{ takes M. Agent Systems}\}
\end{aligned}\]
- $\vert \text{Students}\vert =100$
- $\vert S\vert =40$
- $\vert M\vert = 80$
- $\vert S\cap M\vert =25$
$40+80-25=95=\vert S\cup M\vert $
$\vert \sim(S\cup M)\vert =100-95=5$
Therefore, 5 students took neither as they were part of the universal set but not part of the union of the two subsets.
Computing the Cardinality of a Union of Three Sets
If $A$, $B$ and $C$ are sets then:
\[\begin{aligned}
\vert A\cup B \cup C\vert &= \vert A\vert +\vert B\vert + \vert C\vert\\
&- \vert A\cap B\vert -\vert A\cap C\vert - \vert B\cap C\vert\\
&+ \vert A\cap B\cap C\vert
\end{aligned}\]
This and the last union are special cases of the principle of inclusion and exclusion.
Principle of Inclusion and Exclusion
Let $A_1,A_2,\ldots,A_n$ be sets.
Then:
\[\begin{aligned}
\left\vert A_1\cup\ldots\cup A_n\right\vert =&\sum_{1\leq k\leq n} \left\vert A_i\right\vert -\sum_{1\leq j\leq k\leq n} \left\vert A_j \cap A_k\right\vert\\
&+\sum_{1\leq i\leq j\leq k\leq n} \left\vert A_i \cap A_j \cap A_k\right\vert\\
&-\ldots+(-1)^{n-1}\left\vert A_1\cap\ldots\cap A_n\right\vert
\end{aligned}\]
Why is this set theory “Naive”? The reason is that is suffers from paradoxes.
A barber is the man who shaves all those, and only those, men who do not shave themselves.
This statement and question form a paradox.
As yet we know that you should always write a predicate like so:
\[\{x\in A \vert x \text{ satisfies some property}\}\]
Before Russell sets were just defined by their properties.
Russell’s Paradox shows that the ‘object’ $\{x\vert P(x)\}$ is not always meaningful.
Set $A=\{B\vert B\notin B\}$
Problem: do we have $A\in A$?
Abbreviate, for any set $C$, by $P(C)$ the statement $C\notin$. Then $A=\{B\vert P(B)\}$.
- If $A\in A$, then (from the definition of $P$), not $P(A)$. Therefore $A\notin A$.
- If $A\notin A$, then (from the definition of $P$), $P(A)$. Therefore $A\in A$.
This is the same contradiction that was reached in the opening statement.
This is the reason why we must draw the elements from another set to avoid this paradox. For example, in the definition of even numbers the predicate draws from the set of natural numbers:
\[x\in \mathbb{N} \vert x=2k\ \text{for some int. }k\]
Basics and Definitions
A function is a method that takes an input value and gives an output value:
graph LR
x -->|Input| F[Function Machine]
F -->|Output| fx
A function from a set $A$ to a set $B$ is an assignment of exactly one element of $B$ to each element of $A$.
We write $f(a)=b$ if $b$ is the unique element of $B$ assigned by the function $f$ to the element of $a$.
If $f$ is a function from $A$ to $B$ we write $f: A\rightarrow B$.
graph LR
subgraph x
1
2
3
end
subgraph fx
4
5
6
end
1 --> 4
2 --> 5
3 --> 4
6
A function $f:\{1,2,3\} \rightarrow \{4,5,6\}$.
For every value on the left there should be a single value associated to it on the right.
Domain, Co-domain & Range
Suppose $f:A\rightarrow B$
- $A$ is called the domain of $f$.
- $B$ is called the co-domain fo $f$.
- The range $f(A)$ of $f$ is $f(A)=\{f(x)\vert x\in A\}$.
Co-domain v.s. Range
The difference between co-domain and range is that the co-domain is all values in the set $B$ and the range is all the values, $f(x)$, that $A$ maps to via the function $f$.
graph LR
subgraph B
fA
end
A -->|f| fA
The range of $f$.
Example
Give the range of the function:
\[\sin(x):\mathbb{R}\rightarrow\mathbb{R}\]
The range of the function would be:
\[\sin(x)=\{x\in\mathbb{R}\vert -1\leq x\leq 1\}\]
Composition of Functions
If $f:X\rightarrow Y$ and $g:Y\rightarrow Z$ are functions, then their composition $g\circ f$ is a function from $X$ to $Z$ given by:
\[(g\circ f)(x)=g(f(x))\]
```mermaid
graph LR
subgraph X
x
end
subgraph Y
subgraph Y’
fx
end
end
subgraph Z
gfx
end
x –> fx
fx –> gfx
x –> gfx
X –>|f| Y
Y –>|g| Z
Injective (one-to-one) Functions
Let $f:A\rightarrow B$ be a function. We call $f$ and injective, or one-to-one, function if:
\[f(a_1)=f(a_2)\Rightarrow a_1 = a_2 \text{ for all } a_1,a_2\in A\]
This is logically equivalent to $a_1\neq a_2 \Rightarrow f(a_1) \neq f(a_2)$ and so injective functions never repeat values. In other words:
Different inputs give different outputs.
Example 1
$f:\mathbb{Z}\rightarrow \mathbb{Z}$ given by $f(x)=x^2$ is not injective.
$h:\mathbb{Z}\rightarrow \mathbb{Z}$ given by $h(x)=2x$ is injective.
Example 2
To prove that a function is not injective you can give an individual example of a double mapping.
Take the following question foe the opposite:
$h:\mathbb{Z}\rightarrow \mathbb{Z}$ given by $h(x)=2x$ is injective.
Proof
Suppose for a proof by contradiction that there exist $a_1,a_2$ such that $h(a_1=h(a_2)$ and $a_1\neq a_2$.
$2\times a_1 = 2a_2 \Rightarrow a_1 = a_2$, a contradiction.
Surjective (or onto) Functions
$f:A\rightarrow B$ is surjective, or onto, if the range of $f$ coincides with the co-domain $f$. This means that for every $b\in B$ there exists an $a\in A$ with $b=f(a)$.
Examples
$h:\mathbb{Z}\rightarrow \mathbb{Z}$ given by $h(x)=2x$ is not surjective.
This is because you get every even values out as an answer.
$h’:\mathbb{Q}\rightarrow \mathbb{Q}$ given by $h’(x)=2x$ is surjective.
This is as you can use rational numbers to make any other number when doubled.
Question
Classify $f:\{a,b,c\}\rightarrow\{1,2,3\}$ given by:
graph LR
subgraph x
a
b
c
end
subgraph fx
1
2
3
end
a --> 1
b --> 1
c --> 3
2
- It is a function.
- Not injective, $f(a)=f(b)=1$
- Not subjective as no $x$ maps with $f(x)=2$.
Bijections
We call $f$ bijective if $f$ is both injective and surjective.
Examples
$f:\mathbb{Q}\rightarrow \mathbb{Q}$ given by $f(x)=2x$ is bijective.
Inverse Functions
If $f$ is a bijection from a set $X$ to a set $Y$, then there is a function $f^{-1}$ from $Y$ to $X$ that undoes the action of $f$; that is, it sends each element of $Y$ back to the element of $X$ that it came from. This function is called the inverse function for $f$.
Then $f(a)=b$ if, and only if, $f^{-1}(b)=a$
Example
$k:\mathbb{R}\rightarrow \mathbb{R}$ given by $k(x)=4x+3$ is invertible and $k^{-1}(y)=\frac{1}{4}(y-3)$.
$y=4x+3$. So $4x+3=y$, $4x=y-3$, $x = \frac{y-3}{4}$
This proves the statement by giving the same value.
Cardinality of Finite Sets and Functions
The cardinality of a finite set $S$ is the number of elements in $S$.
A bijection $f:S\rightarrow\{1,\ldots,n\}$. This means that there are as many elements in the set that $S$ maps to as there are in $S$.
For finite sets $A$ and $B$:
- $\vert A\vert \geq\vert B\vert \Rightarrow$ there is a surjective function from $A$ to $B$.
- $\vert A\vert \leq\vert B\vert \Rightarrow$ there is an injective function from $A$ to $B$.
- $\vert A\vert =\vert B\vert \Rightarrow$ there is a bijection function from $A$ to $B$.
graph TD
subgraph A
a[ ]
b[ ]
c[ ]
end
subgraph n1[n]
1
2
n
end
subgraph B
d[ ]
e[ ]
f[ ]
end
a --> 1
b --> 2
c --> n
d --> 1
e --> 2
f --> n
From the graph as $\vert A\vert =n=\vert B\vert$ then we can deduce that $g^{-1}\circ f$.
- Bijective means one to one.
- Surjective means many to one.
- Injective means one to many.
The Pigeonhole Principle
Let $f:A\rightarrow B$ be a function where $A$ and $B$ are finite sets.
The pigeonhole principle states that if $\vert A\vert >\vert B\vert$ then at least one value of $f$ occurs more than once.
In other words, we have $f(a)=f(b)$ for some distinct elements $a,b$ of $A$.
The principle is if $(N+1)$ pigeons occupy $N$ holes, then some hole must have at least 2 pigeons.
Example 1
There are 15 people on a bus. Show that at least two of them have a birthday in the same month of the year.
Proof
Let $A$ be the set of all people on the bus. $\vert A\vert =15$
Let $B$ be the set of months. $\vert B\vert =12$
$f$ associates the month in which a person has been born with that person.
By the pigeonhole principle (PHP), at least two of them have a birthday on the same day.
Example 2
How many different surnames must appear in a telephone directory to guarantee that at least two of the surnames begin with the same letter of the alphabet and end with the same letter of the alphabet?
If we are solving this by the pigeonhole principle then the set $A$ of names must have same cardinality as $\vert B\vert +1$ where $B$ is the set of all pairs of letters.
$\vert B\vert =26^2$
Therefore
$\vert B\vert +1=26^2+1$
Example 3
Five number are selected from the numbers $1,2,3,4,5,6,7$ and $8$. Show that there will always be two of the numbers that sum to $9$.
Proof
graph LR
subgraph B
1[1,8]
2[2,7]
3[3,6]
4[4,5]
end
subgraph A
x1
x2
x3
x4
x5
end
x1 --> 1
x2 --> 2
x3 --> 3
x4 --> 4
x5 --> 1
$\vert A\vert =5$ and $\vert B\vert =4$. If each element with $x_n$ maps to the pair which contains its digit then there must be a pair with more than one mapping. This is to say that the two sets maps via a surjective function.
This proves that there will always be one pair in the list that sums to 9.
Extended Pigeonhole Principle
Consider a function $f:A\rightarrow B$ where $A$ and $B$ are finite sets and $\vert A\vert >k\vert B\vert$ for some natural number $k$. Then, there is a value of $f$ which occurs at least $k+1$ times.
graph TD
subgraph A
a
b
c
d
e
f
g
end
subgraph B
1
2
3
end
a --> 1
b --> 2
c --> 3
d --> 1
e --> 2
f --> 3
g --> 1
In this graph $k=2$. Additionally you can see that the value 1 occurs $k+1=3$ times as $a,d$ and $g$ all map to it.
Example
How many different surnames must appear in a telephone directory to guarantee that at least five of the surnames begin with the same letter of the alphabet and end with the same letter of the alphabet?
graph LR
subgraph A
Names
end
subgraph B
a,a
...
end
Names --> a,a
Names --> ...
$\vert B\vert =26^2$
Therefore:
Due to the principles covered above, $\vert A\vert >4\vert B\vert $
Thus:
$\vert A\vert =4\times26\times26+1=2705$
Theorem of Friends and Strangers
Show that in any group of six people there are either three who all know each other or three complete strangers.

On this graph blue is people who know each other and red is people who don’t. From the graph you can see that only two people will know each other.
What the question is saying is that no matter how you colour this you will always have a triangle of three people with red lines (don’t know) or blue lines (do know).
Proof
Let $A,B,C,D,E,\underline F$ denote people under consideration.
Construct $f:\{A,B,C,D,E\}\rightarrow\{0,1\}$ as follows: $f(x)=1$ if $x$ knows $F$, or $0$ else.
This means that we are taking out the person $F$ and considering who they know in a binary format.
graph TD
subgraph 2[A]
A
B
C
D
E
end
subgraph 3[B]
0
1
end
$\vert A\vert =5, \vert B\vert =2$ Therefore there must exist $\{x_1,x_2,x_3\}\subseteq\{A,B,C,D,E\}$ such that $f(x_1)=f(x_2)=f(x_3)$
Case 1
Suppose that $f(x_1)=f(x_2)=f(x_3)=1$. This means that they all know each other.
graph LR
x1 --> F
x2 --> F
x3 --> F
x2 -->|Case 1.1| x3
x1 .->|Case 1.2| x2
x2 .->|Case 1.2| x3
x3 .->|Case 1.2| x1
Dotted means don’t know.
Case 1.1
There is a pair who know each other.
Case 1.2
There is no pair who know each other.
So $x_1,x_2,x_3$ are complete strangers.
Case 2
$f(x_1)=f(x_2)=f(x_3)=0$
graph LR
x1 .-> F
x2 .-> F
x3 .-> F
x1 -->|Case 2.1| x2
x2 -->|Case 2.1| x3
x3 -->|Case 2.1| x1
x1 .->|Case 2.2| x2
Dotted means don’t know.
Case 2.1
$x_1,x_2,x_3$ all know each other.
Case 2.2
Three is a pair who don’t know each other.
As you can see in any case there is a triangle of three people with links stating that they know or don’t know each other in any case. This proves the statement. This is as we can see that three know or don’t know each other in any situation.
Power Sets
The power set $\text{Pow}\{A\}$ of a set $A$ is the set of all possible subsets. This includes the null set $\emptyset$ and the full set.
Each set in the power set follows this definition:
\[\{x\vert x\subseteq A\}\]
Example
The power set $\text{Pow}\{A\}$ of a set $A=\{1,2\}$ is:
\[\{\emptyset,\{1\},\{2\},\{1,2\}\}\]
For any set $A$:
\[\vert \text{Pow(A)}\vert =2^{\vert A\vert }\]
Therefore:
\[\{x\vert x\in\text{Pow}(A)\}=\{\emptyset,\ldots\}\]
Russell’s Paradox
People say that you can define a set just by defining the constraints of the set:
\[\{x\in\mathbb{R}\vert x<4,x\geq-1\}\]
However statements written in this way are susceptible to paradoxes. For example the following paradox:
Everyone from Crete is a liar. (Said by a person from Crete)
Paradoxes in General
A paradox is a case that when expanded contains a contradiction.
Avoiding Paradoxes
To avoid paradoxes we should write the set definition in the following way:
\[\{x\in\ldots\vert \ldots\}\]
This means that the set or value x should be taken from some other set.
They should not be written like this:
\[\{x\ldots\vert \ldots\}\]
Venn Diagrams and Set Logic
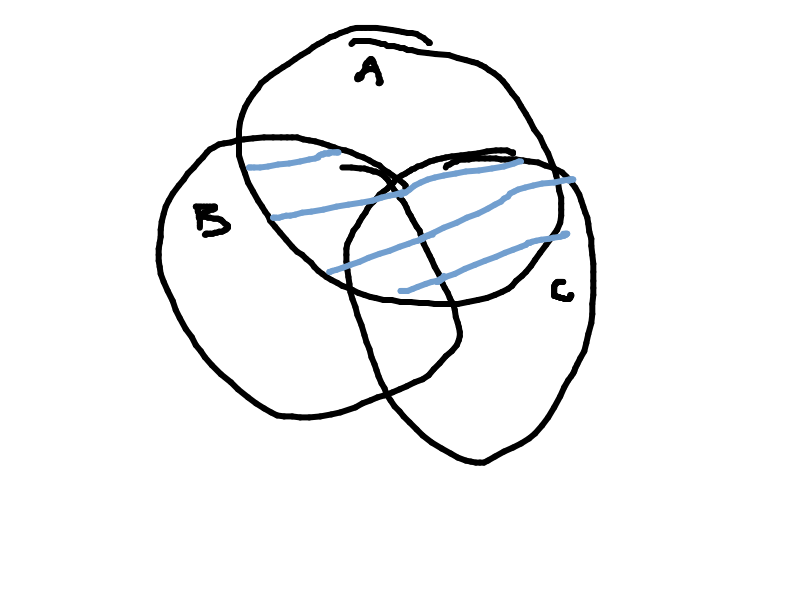
Draw the following as a Venn diagram: $A\cap (B\cup C)$
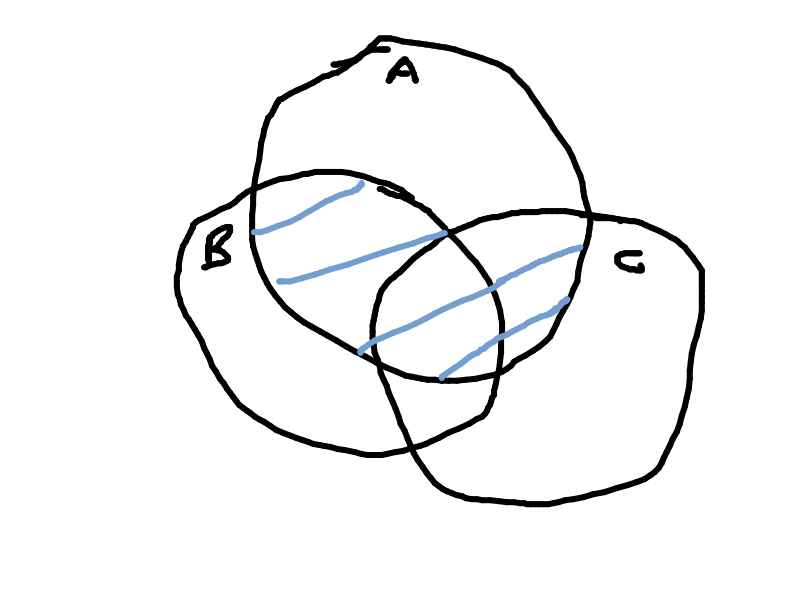
Draw the following as a Venn diagram: $(A\cap B)\cup(A\cap C)$
Bijections and Cardinality
The cardinality of a finite set is the number of element in the set. Sets $A$ and $B$ have the same cardinality $\Rightarrow$ there is a bijection from $A$ to $B$.
Let $S=\{1,2,\ldots,n\}$ and let $B^n$ be the set of bit strings of length $n$. The function:
\[f:\text{Pow}(S)\rightarrow B^n\]
assigns each subset $A$ of $S$ to its characteristic vector is a bijection.
We used this to compute the cardinality of the powerset.
Infinite Sets
Sets $A$ and $B$ have the same cardinality iff there is a bijection from $A$ to $B$.
$\mathbb{Z}$ and even integers.
$S=\{n\in\mathbb{Z}\vert n\text{ is even}\}$
$f:\mathbb{Z}\rightarrow S$
$f(n)=2n$
$f$ is a bijection
This is by the definition of bijection as the function maps one to one.
Hilberts Infinite Hotel
$\mathbb{N}$ and $\mathbb{Z}$
Consider a hotel with rooms and a train with people having the cardinality $\in \mathbb{N^+}$. Each person in the train is given a unique room.
A second train arrives with the same properties. Consider that people in train one are given odd rooms and people in train two are given even rooms.
The relation between the cardinality of the hotel and the two trains:
$f:\mathbb{Z}\rightarrow\mathbb{N}$
\[f(n) = \begin{cases}2n,& \text{if } n\geq 0\\ -2n-1,& \text{if }n<0\end{cases}\]
This proves that there is a bijection between the two sets $\mathbb{Z}$ (the integers) and $\mathbb{N}$ (natural numbers).
Real numbers $\{x\in\mathbb{R}\vert o<x<1\}$ and $\mathbb{R^+}$
x-axis:
label: x
range: -10 10
y-axis:
label: g(x)=1/x-1
range: -3 3
plot:
x: range: -10 10 200
y: math: x^(-1)-1
plot:
x: 0
y: -3 3
color: black
plot:
x: -11 11
y: 0 0
color: black
plot:
x: 1 1
y: -3 3
color: blue
This graph shows that there is a one to one mapping of the numbers between 0 and 1 to all real numbers. This is becuse for all values for x between 0 and one all real numbers are produced on the y axis.
Countable Sets
A set that is either finite or has the same cardinality as $\mathbb{N}$ is called countable.
$\mathbb{Z}$
For a set $\mathbb{Z}$ you can count it by starting at zero and then jumping from item to item by the way of a function. In this way you can produce the following mapping: $\mathbb{Z}\rightarrow\mathbb{N}$.
$\mathbb{Q}$
Consider an infinite table like so:
| $\frac{1}{1}$ |
$\frac{1}{2}$ |
$\frac{1}{3}$ |
$\ldots$ |
| $\frac{2}{1}$ |
$\frac{2}{2}$ |
$\frac{2}{3}$ |
$\ldots$ |
| $\frac{3}{1}$ |
$\frac{3}{2}$ |
$\frac{3}{3}$ |
$\ldots$ |
| $\ldots$ |
$\ldots$ |
$\ldots$ |
$\ddots$ |
In this table each number is represented infinitely many times due to equivalencies.
Start counting in the top left corner. Then count from the first diagonal from top to bottom. For equivalent elements there is no need to count them as the set only includes the most simplified fraction.
From this you can conclude that the cardinality of the set of rational numbers is a bijection of the set of natural numbers. This means that it is countable.
Uncountable Sets
A set that is not countable is called uncountable. The following set is uncountable:
\[S = \{ x \in \mathbb{R} \vert 0 < x < 1 \}\]
There is no bijective function from this set to the set of all natural numbers.
Cantor’s Diagonal Argument
Suppose for a proof by contradiction that there exists a bijection $f:\mathbb{N^+}\rightarrow S$. Consider decimal representation of $f(n)$, for $n\in\mathbb{N^+}$:
In this example we are proving for all decimals between 0 and 1. We are considering that there is a mapping that makes them countable.
- $f(1)=0.a_{11}a_{12}a_{13}\ldots a_{1n}\ldots$
- $f(2)=0.a_{21}a_{22}a_{23}\ldots a_{2n}\ldots$
- $f(3)=0.a_{31}a_{32}a_{33}\ldots a_{3n}\ldots$
- $\vdots$
- $f(n)=0.a_{n1}a_{n2}a_{n3}\ldots a_{nn}\ldots$
- $\vdots$
In this proof we treat this as a table without the leading zero and consider the main diagonal where the digit $a_{ij}$ has equal $i$ and $j$.
We show that there exists $d\in S$ such that for no $i\in\mathbb{N^+}$ we have $f(i)=d$.
Let $d=0.d_{1}d_{2}d_{3}\ldots d_{n}\ldots$ where $d_i=\begin{cases}2, & \text{if } a_{ii}=1\ 1, & \text{if } a_{ii}\neq 1\end{cases}$
Then for every $i\in\mathbb{N^+}$ $d$ is different at position $i$ from $f(i)$. So, for no $i\in\mathbb{N^+}$ we have $f(i)=d$, fo $f$ is not surjective. A contradiction.
Cartesian Product
For the Cartesian product you are making a list of all possibilities of the elements in both sets. This is similar to multiplying brackets.
Example
Let $A=\{1,2\}$ and $B=\{a,b,c\}$, then:
\[A\times B = \{(1,a),(2,a),(1,b),(2,b),(1,c),(2,c)\}\]
Therefore:
\[B\times A = \{(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)\}\]
Relations
Any relation between the elements in set $A$ and $B$ will be in the set of their Cartesian product.
A binary relation between two sets $A$ and $B$ is a subset $R$ of the Cartesian product $A\times B$.
If $A=B$, then $R$ is called a binary relation on $A$.
Family Tree Example
The set $A$ is the set of all people in the tree.
graph TD
fm[Fred and Mavis] --- Alice
fm --- ks[Ken and Sue]
ks --- Jane
ks --- Fiona
ks --- Alan
jm[John and Mary] --- ks
jm --- Mike
jm --- Penny
-
$R=\{(x,y)\vert x\text{ is a grandfather of } y\}$
For this set:
\[R=\{\text{(Fred, Jane), (Fred, Fiona),}\text{ (Fred, Alan), (John, Jayne),}\text{ (John, Fiona), (John, Alan)}\}\]
-
$S=\{(x,y)\vert x\text{ is a sister of } y\}$
For this set:
\[S=\{\text{(Alice, Ken), (Sue, Mike),}\text{ (Sue, Penny), (Penny, Sue),}\text{ (Penny, Mike), (Jane, Fiona)}\}\]
Algebraic Example
Write down the ordered parts belonging to the following binary relations between $A=\{1,3,5,7\}$ and $B=\{2,4,6\}:$
-
$U=\{(x,y)\in A\times B \vert x + y = 9\}$
This means the combinations from the two sets where the elements sum to 9.
$U=\{(3,6),(5,4),(7,2)\}$
-
$V=\{(x,y)\in A\times B \vert x < y \}$
This is the set of all pairs such that the first element is smaller than the second element:
\[V=\{(1,2),(1,4),(1,6),(3,4),(3,6),(5,6)\}\]
Digraph Representation of Relations
Recall that a function $f$ from a set $A$ to a set $B$ assigns exactly one element of $B$ to each element of $A$.
- Gives rise to the relation $R_f=\{(a,b)\in A\times B \vert b =f(a)\}$
If a relation $S\subseteq A\times B$ is such that for every $a\in A$ there exists at most one $b\in B$ with $(a,b)\in S$, relation $S$ is functional.
Sometimes in the literature, functions are introduces through functional relations.
Example
$A\{i\in \Bbb{N}\vert i<10\},B=\{i\in\Bbb{N}\vert 5<i<15\},$$\ R=\{((x,y)\in A\times B\vert y =2x)\}$
graph TD
subgraph A
0
1
2
3
4
5
6
7
8
9
end
subgraph B
62[6]
72[7]
82[8]
92[9]
10
11
12
13
14
end
3 --> 62
4 --> 82
5 --> 10
6 --> 12
7 --> 14
As this is a relation there are allowed to be values in the set $A$ which don’t have a mapping to a value in the set $B$. If this was a function and not a relation that wouldn’t be allowed.
This is a functional relation as each item in $A$ only has one mapping to $B$.
Building New Relations from Given Ones
Inverse Relation
Given a realtion $R\subseteq A \times B$. We define the inverse relation $R^{-1}\subset B\times A$ by:
\[R^{-1}=\{(b,a)\vert (a,b) \in R\}\]
Example:
- The inverse of the relation is a parent of on the set of people is the relation is a child of.
In other words if you swap the elements of a given relation you should get the inverse relation.
Example
$A=\{1,2,3,4\},R=\{(x,y)\vert x\leq y\}$
Therefore:
$R=\{(1,1),(1,2),(1,3),(1,4),$$(2,2),(2,3),(2,4),(3,3),(3,4),(4,4)\}$
And:
$R=\{(1,1),(2,1),(3,1),(4,1),$$(2,2),(3,2),(4,2),(3,3),(4,3),(4,4)\}$
You could also say:
$R^{-1}=\{(y,x)\vert x \leq y\} = \{(u,v)\vert u\geq v\}$
In these examples you either swap the predicate to denote the inverse or you swap the evaluation such that it produces the inverse.
Composition of Relations
Let $R\subseteq A\times b$ and $s\subseteq B\times C$. The (functional) composition of $R$ and $S$, denoted by $S\circ R$, is the binary relation between $A$ and $C$ given by: $S\circ R =\(\\{(a,c)\vert \text{ exists } b\in B \text{ such that }\)aRb \text{ and } bSc\}$
The notation $aRb$ is another way of writing $(a,b)\in R$.
graph LR
subgraph A
a[1]
end
subgraph B
b[ ]
end
subgraph C
c[2]
end
a -->|R subset A * B| b
b -->|S subset B * C| c
Example:
- If $R$ is the relation is a sister of and $S$ is the relation is a parent of then:
- $S\circ R$ is the relation is an aunt of.
- $S\circ S$ is the relation is a grandparent of.
Example
- $R:$ is a sister of
- $S:$ is a parent of
- $S\circ R=\{(a,c)\vert\text{ exists } b\in B\text{ such that }$$ aRb \text{ and } bSc\}$
graph TD
fm[Fred and Mavis] --- Alice
fm --- ks[Ken and Sue]
ks --- Jane
ks --- Fiona
ks --- Alan
jm[John and Mary] --- ks
jm --- Mike
jm --- Penny
- Alice $R$ Ken and Ken $S$ Alan so Alice $S\circ R$ Alan.
- This can also be written as $(\text{Alice, Alan})\in S\circ R$
Diagraph Representation of Compositions
For this diagram $A=\{a,b\},B=\{1,2,3\},C=\{x,y\}$:
graph LR
subgraph R
a --> 1
a --> 2
b --> 2
a --> 3
end
subgraph S
12[1] --> y
22[2] --> x
32[3] --> x
end
subgraph S circ R
a2[a] --> x2[x]
a2 --> y2[y]
b2[b] --> x2
end
1 --> 12
2 --> 22
3 --> 32
Computer Friendly Representation of Binary Relations - Matrices
Let $A=\{a_1,\ldots,a_n\},B=\{b_1,\ldots,b_m\}$ and $R\subseteq A\times B$.
We represent $R$ by an array $M$ of $n$ rows and $m$ columns. Such an array is called an $n$ by $m$ matrix.
The entry in row $i$ and column $j$ of this matrix is given by $M(i,j)$ where:
\[M(i,j)=\begin{cases}
1 & \text{ if } (a_i,b_j)\in R\\
0 & \text{ if } (a_1,b_j)\notin R
\end{cases}\]
Example 1
Let $A=\{1,3,5,7\}, B=\{2,4,6\}$ and:
\[U=\{(x,y)\in A\times B\vert x + y = 9\}\]
Assume an enumeration $a_1=1,a_2=3,a_3=5,a_4=7$ and $b_1=2,b_2=4,b_3=6$. Then $M$ represents $U$, where:
\[M = \begin{bmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & 1 & 0\\
1 & 0 & 0
\end{bmatrix}\]
When representing in a matrix the rows are the items in set $A$ going down and the columns are the items in set $B$ going across.
You can then read the answers from the matrix as: $U=\{(7,2),(5,4),(4,6)\}$.
Example 2
The binary relation $R$ on $A=\{1,2,3,4\}$ has the following digraph representation:
graph LR
4 --> 3
3 --> 2
2 --> 1
-
What are the ordered pairs?
$R=\{(4,3),(3,2),(2,1)\}$
-
Draw the matrix.
\[\begin{bmatrix}
0&0&0&0\\
1&0&0&0\\
0&1&0&0\\
0&0&1&0
\end{bmatrix}\]
-
Explain the relation.
$x$ is 1 larger than $y$.
Matrices and Composition
This is working on the same relation as was seen in the section Diagraph Representation of Compositions.
graph LR
subgraph X
a
b
end
subgraph Y
1
2
3
end
subgraph Z
x
y
end
a --> 1
a --> 2
a --> 3
b --> 2
1 --> y
2 --> x
3 --> x
This result in the following for the composition of $S\circ R$:
graph LR
a --> x
a --> y
b --> x
From these graphs we can deduce that $R\subseteq X\times Y, S\subseteq Y\times Z$.
Given the matrices of $R$ and $S$:
\[R: \begin{bmatrix}
1&1&1\\
0&1&0
\end{bmatrix}
S: \begin{bmatrix}
0&1\\
1&0\\
1&0
\end{bmatrix}\]
Calculate the binary relation matrix of $S\circ R$:
If you transpose the row $a$ in the matrix $R$ on the column $x$ in the matrix $S$ you can compare to see of $a$ is a subset of $y$. If it is then you put a 1 in the resultant matrix and if not you put a zero:
\[S\circ R:\begin{bmatrix}
1&1\\
1&0
\end{bmatrix}\]
Boolean Matrix Product
Given two matrices with entries 1 and 0 representing the relations we can form the matrix representing the composition. This is called the logical (Boolean) matrix product.
Let $A=\{a_1,\ldots,a_n\},B=\{b_1,\ldots,b_m\}$ and $C=\{c_1,\ldots,c_p\}$.
The logical matrix $M$ representing $R$ is given by:
\[M(i,j)=\begin{cases}
1 & \text{ if } (a_i,b_j)\in R\\
0 & \text{ if } (a_1,b_j)\notin R
\end{cases}\]
The logical matrix $N$ representing $S$ is given by:
\[N(i,j)=\begin{cases}
1 & \text{ if } (b_i,c_j)\in S\\
0 & \text{ if } (b_1,c_j)\notin S
\end{cases}\]
Then the entries $P(i,)$ of the logical matrix $P$ representing $S\circ R$ are given by:
- $P(i,j)=1$ if there existsw $l$ with $1\leq l\leq m$ such that $M(i,l)=1$ and $N(i,j)=1$.
- $P(i,j)=0$, otherwise.
This is the same as a product of matrices, $P=MN$. Instead of addition and multiplication we use logical OR and AND.
Properties of Relations on a Set
Infix Notation for Binary Relations
If $R$ is a binary relation then we write $xRy$ whenever $(x,y)\in R$. The predicate $xRy$ is read as $x$ is $R$-related to $y$.
This is similar to the notation $a\subseteq b$ or $a\leq b$.
Comparing Strings
Consider relations $R,S$ and $L$ on the set of all strings:
- $R$-lexicographic ordering.
- This is alphabetic ordering.
- $uSv$ if, and only if, $u$ is a sub-string of $v$.
- $\text{an}S\text{ana},\ \text{ana}S\text{banana}$.
- $uSv,\ vSw\Rightarrow uSw$.
- This means that for any ordering such as $u$ then $v$ the ordering of $u$ and $w$ is also true provided that we know that $v<w$.
- $uLv$ if, and only if, $\text{len}(u)\leq \text{len}(v)$.
For any of these relations:
\[\forall u,v \text{ if } uRv \text{ and } vRu\Rightarrow u=v\]
This means if the relation works both ways then they are equal in terms of the ordering.
Properties of Binary Relations
A binary relation $R$ on a set $A$ is:
Reflexive
When $xRx$ for all $x\in A$.
\[\forall x\ A(x)\Rightarrow xRx\]
This means that if two of the same elements are compared successfully then the relation is reflexive.
As example of a relation that is non-reflexive is $<$ as the left must be different to the right.
Symmetric
When $xRy$ implies $yRx$ for all $x,y\in A$:
\[\forall x,y\ xRy\Rightarrow yRx\]
This is similar to Facebook friends. If you are friends with one person they have to be your friend too.
An example that is non-symmetric is $\leq$ as they are not necessarily comparable.
Antisymmetric
When $xRy$ and $yRx$ imply $x=y$ for all $x,y\in A$:
\[\forall x,y\ xRy\text{ and } yRx\Rightarrow y = x\]
This means that if you can swap the elements and the relation still holds true then the elements must be equal. This is the same as the $\leq$ relation.
The $L$ relation from before doesn’t satisfy this property as two different words with the same length are not the same.
Transitive
When $xRy$ and $yRz$ imply $xRz$ for all $x,y,z\in A$:
\[\forall x,y,z\ xRy\text{ and }yRz\Rightarrow xRz\]
This is the same as the ordering example from before. Thus the relationship $<$ satisfies this property.
Examples
Which of the following define a relation that is reflexive, symmetric, antisymmetric of transitive?
- $x$ divides $y$ on the set $\Bbb{Z^+}$ of positive integers.
- This relations is reflexive, antisymmetric and transitive.
- $x\neq y$ on the set $\Bbb{Z}$ of integers.
- This relations is symmetric and transitive.
- $x$ has the same age as $y$ on the set of people.
- This relations is reflexive, symmetric and transitive.
Digraph Representation
In the directed graph representation, $R$ is:
- Reflexive if there is always an arrow from every vertex to itself.
- Symmetric if whenever there is an arrow from $x$ to $y$ there is also an arrow from $y$ to $x$.
- Antisymmetric if whenever there is an arrow from $x$ to $y$ and $x\neq y$, then there is no arrow from $y$ to $x$.
- Transitive if whenever there is an arrow from $x$ to $y$ and from $y$ to $z$ there is also an arrow from $x$ to $z$.
Example 1
Let:
\[\begin{aligned}
A=&\{1,2,3\}\\
R_1=&\{(1,1),(2,2),(3,3),(2,3),(3,2)\}
\end{aligned}\]
graph TD
1((1)) --> 1
2((2)) --> 2
3((3)) --> 3
2 --> 3
3 --> 2
Example 2
Let:
\[\begin{aligned}
A&=\{1,2,3\}\\
R_1&=\{(2,2),(2,3),(3,2),(3,3)\}
\end{aligned}\]
graph TD
1((1))
2((2)) --> 2
3((3)) --> 3
2 --> 3
3 --> 2
Example 3
Let $A={1,2,3},R_1={(1,1),(2,2),(3,3),(1,3)}$
graph TD
1((1)) --> 3
1 --> 1
2((2)) --> 2
3((3)) --> 3
- Reflective $\forall x:xRx$
- Symmetric $\forall x,y: xRy\Rightarrow yRx$
- Antisymmetric $\forall x,y:xRy,yRx\Rightarrow x=y$
- Transitive $\forall x,y,z:xRy,yRz\Rightarrow xRz$
Example 3
Let $A=\{1,2,3\},R_1=\{(1,3),(3,2),(2,3)\}$
graph TD
1((1)) --> 3
3((3)) --> 2
2((2)) --> 3
- Reflective $\forall x:xRx$
- Symmetric $\forall x,y: xRy\Rightarrow yRx$
- Antisymmetric $\forall x,y:xRy,yRx\Rightarrow x=y$
- Transitive $\forall x,y,z:xRy,yRz\Rightarrow xRz$
Example - Reachability
Consider some roads in a city. Some may be private and not link up, some may be one way, some may have no stopping. This is represented on the following graph:
graph TD
1((1)) --> 2((2))
2 --> 6((6))
6 --> 4((4))
4 --> 5((5))
5 --> 5
4 --> 1
1 --> 4
3((3)) --> 3
Say you start at 1 and end at 5 are you able to make this path?
If there was a transitive relation from the source to the destination then you would be able to get there in one hop.
This will be continued in the next lecture.
Transitive Closure
Given a binary relation $R$ on a set $A$ the transitive closure $R^*$ of $R$ is the (uniquely determined) relation on $A$ with the following properties:
Simple Example
You are given the following links. What links are missing to make the relation transitive.
graph LR
a((a)) --> b((b))
b --> c((c))
As there is an arrow from $a$ to $b$ and an arrow from $b$ to $c$ there should be and arrow from $a$ to $c$ to make this transitive.
graph LR
a((a)) --> b((b))
b --> c((c))
a -.-> c
Example 1
Let $A=\{1,2,3\}$. Find the transitive closure of:
\[R=\{(1,1),(1,2),(1,3),(2,3),(3,1)\}\]
This relation has the following graph:
graph LR
1((1)) --> 1
1 --> 2((2))
1 --> 3((3))
2 --> 3
3 --> 1
You should add the following links:
graph LR
1((1)) --> 1
1 --> 2((2))
1 --> 3((3))
2 --> 1
3 --> 2
2 --> 3
3 --> 1
3 --> 3
2 --> 2
Transitivity and Composition
A relation $S$ is transitive if and only if $S\circ S\subseteq S$. This is because:
\[S\circ S=\{(a,c)\vert \text{ exists } b \text{ such that } aSb \text{ and } bSc\}\]
This is the definition of what the composition of a relation is.
Let $S$ be a relation. Set $S^1=S,S^2=S\circ S,S^3=S\circ S\circ S\circ S$ and so on.
Theorem
Denote by $S^$ the transitive closure of $S$. Then $xS^y$ if and only if there exists $n>0$ such that $xS^ny$.
This theorem states that by repeating Warshall’s algorithm on your matrix until there is no change then you will reach transitive closure for that relational matrix.
The relation $R$ on the set $A=\{1,2,3,4,5\}$ is represented by the matrix:
\[\begin{bmatrix}
1&0&0&1&0\\
0&1&0&0&1\\
0&0&1&0&0\\
1&0&1&0&0\\
0&1&0&1&0
\end{bmatrix}\]
Determine the matrix $R\circ R$ and hence explain why $R$ is not transitive.
To compute this we transpose the row $i$ onto the column $j$ and see if there are two ones in the same position. If this is the case then the resultant matrix has a 1 in row $i$ and column $j$. If not then there is a zero:
\[\begin{aligned}
&\begin{bmatrix}
1&0&0&1&0\\
0&1&0&0&1\\
0&0&1&0&0\\
1&0&1&0&0\\
0&1&0&1&0
\end{bmatrix}
\begin{bmatrix}
1&0&0&1&0\\
0&1&0&0&1\\
0&0&1&0&0\\
1&0&1&0&0\\
0&1&0&1&0
\end{bmatrix}\\
=&\begin{bmatrix}
1&0&1&1&0\\
0&1&0&1&1\\
0&0&1&0&0\\
1&0&1&1&0\\
1&1&1&0&1
\end{bmatrix}
\end{aligned}\]
$R$ is not transitive as $R^2\neq R$
This is the same as Warshall’s Algorithm. In this algorithm you iterate through every item in each column and row and each column and row. If there is a match you put a 1 in the resultant matrix and if there is not then you put a 0.
Equivalence Relations
A binary relation $R$ on a set $A$ is called an equivalence relation if it is reflective, transitive and symmetric.
This is the same as $x=y$ in that $x$ has the same property as $y$.
Example 1
The relation $R$ on the non-zero integers given by $xRy$ if $xy>0$.
This means that the relation is satisfied if $x$ and $y$ are both positive or both negative.
-
Reflexivity: $\forall x\in \Bbb{Z}-\{0\}$
$x\times x=x^2$
- Symmetry: $\forall x,y\in \Bbb{Z}-\{0\}\text{ if }x\times y>0\text{ then }$$ y\times x =x\times y>0$
-
Transitivity: $\forall x,y,z\in \Bbb{Z}-\{0\}$$\text{ if } xRy\text{ and }yRz \text{ then } xRz$
This is a statement which must be proved in order to be valid. See below.
Suppose that $x,y,z$ are particular but arbitrarily chosen non-zero numbers such that $x\times y>0$ and $y\times z>0$.
Case 1 - $y>0$
$y>0\Rightarrow x>0,z>0\Rightarrow x\times z>0$
Case 2 - $y<0$
$y<0\Rightarrow x<0,z<0\Rightarrow x\times z >0$
Example
Let $f:A\rightarrow B$ be a function. Define a relation $R$ on $A$ by:
\[a_1Ra_2\Leftrightarrow f(a_1)=f(a_2)\]
$A$ is a set of cars, $B$ is the set of real numbers, and $f$ assigns to any car in $A$ its length. Then $a_1Ra_2$ if and only if $a_1$ and $a_2$ are of the same length.
In this case the length of the car is mapped to a real number. They could also be mapped to a word such as $\text{long}$.
Partition of a Set
A partition of a set $A$ is a collection of non-empty subsets $A_1,\ldots A_n$ of $A$ satisfying:
- $A=A-1\cup A_2\cup\ldots\cup A_n$.
- $A_i\cap A_j=\emptyset$ for $i\neq j$.
The $A_i$ are called the blocks of the partition.
graph TD
subgraph A
A1
A2
A3
A4
end
This set $A$ has four blocks and the four blocks cover every element in the set $A$.
This is the same as example 1 where the relation split the set of non-zero real numbers into two blocks of positive and negative numbers.
Equivalence Class
The equivalence class $E_x$ of any $x\in A$ is defined by:
\[E_x=\{y\vert yRx\}\]
From the example before, the equivalence class of any positive integer is the class of positive integers and the equivalence class of any negative integer is the class of all negative integers.
Connecting Partitions and Equivalence Relations
Statement 1
Let $R$ be an equivalence relation on a non-empty set $A$. Then the equivalence classes $\{E_x\vert x\in A\}$ form a partition of $A$.
Proof (Optional)
The proof is in four parts:
-
We show that the equivalence classes $E_x=\{y\vert yRx\},x\in A$, are non-empty subsets of $A$: by definition, each $E_x$ is a subset of $A$. Since $R$ is reflexive, $xRx$. Therefore $x\in E_x$ and so $E_x$ is non-empty.
This means that no equivalence class is not empty. This is because in a reflexive relation there are links to every element.
-
We show that $A$ is the union of equivalence classes $E_x,x\in A$: We know that $E_x\subseteq A$, for all $E_x, x\in A$. Then $x\in E_x$. So, $A$ is a subset of the union of the equivalence classes.
This means that the union of all the classes forms the full set and that they don’t share any elements.
- We show that if $xRy$ then $E_x=E_y$: Suppose that $xRy$ and let $z\in E_x$. Then $zRx$ and $xRy$. Since $R$ is a transitive relation, $zRy$. Therefore, $z\in E_y$. We have shown that $E_x\subseteq E_y$. An analogous argument shows that $E_y\subseteq E_x$. So, $E_x=E_y$.
-
We show that any two distinct equivalence classes are disjoint: To this end we show that if two equivalence classes are not disjoint then they are identical. Suppose $E_x\cup E_y\neq \emptyset$. Take a $z\in E_x\cap E_y$. Then, $zRx$ and $zRy$. Since $R$ is symmetric, $xRZ$ and $zRy$. Bu then, by transitivity of $R$, $xRy$. Therefore, by 3., $E_x=E_y$
These two mean that there can be no different partitions that overlap but don’t contain the same items. By this they must be the same equivalence class or be disjoint (have no elements in common).
Statement 2
Suppose that $A_1,\ldots,A_n$ is a partition of $A$. Define a relation $R$ on $A$ by setting: $xRy$ of an only if there exists $i$ such that $1\leq i\leq n$ and $x,y\in A_i$. Then $R$ is an equivalence relation.
Proof (Optional)
- Reflexivity: if $x\in A$, then $x\in A_i$ for some $i$. Therefore $xRx$.
- Transitivity: if $xRy$ and $yRz$, then there exists $A_i$ and $A_j$ such that $x,y\in A_i$ and $y,z\in A_j$. $y\in A_i\cap A_j$ implies $i=j$. Therefore $x,z\in A_i$ which implies $xRz$.
- Symmetry: if $xRy$, then there exist $A_i$ such that $x,y\in A_i$. Therefore $yRx$.
Application - Rational Numbers
From what we have learned you can define the concept of rational numbers based on the set of integers.
$r$ is rational if $r=\frac{k}{k}$, where $k,l$ are integers and $l\neq 0$.
Evidently, $\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\ldots$
Consider the set $A=\{(a,b)\in\Bbb{Z\times Z}\vert b\neq0\}$ and relation $R$ on $A$ defined as:
\[(a,b)R(c,d)\Leftrightarrow ad=bc\]
- $R$ is an equivalence relation on$A$ and the set of all equivalence classes of.
- $R$ is the set of rationals
In other words:
\[\Bbb{Q}=\{E_x\vert x\in A\}\]
Partial Orders
A binary relation $R$ on set $A$ which is reflexive, transitive and antisymmetric is called a partial order.
Partial orders are important in situations where we wish to characterise precedence.
Examples
- The relation $\leq$ on the set of $\Bbb{R}$ of real numbers.
- The relation $\subseteq$ on $\text{Pow}(A)$.
- “Is a divisor of” on the set $\Bbb{Z^+}$ of positive integers.
Example - Job Scheduling
| Task |
Immediate Dependencies |
| 1 |
|
| 2 |
1 |
| 3 |
1 |
| 4 |
2 |
| 5 |
2, 3 |
| 6 |
4 |
| 7 |
2, 3 |
| 8 |
4, 5 |
| 9 |
6, 7, 8 |
graph LR
1[Task 1 - 7 Hours] --> 2[Task 2 - 6 Hours]
1 --> 3[Task 3 - 3 Hours]
2 --> 4[Task 4 - 6 Hours]
2 --> 5[Task 5 - 3 Hours]
3 --> 5
4 --> 6[Task 6 - 1 Hour]
2 --> 7[Task 7 - 1 Hour]
3 --> 7
4 --> 8[Task 8 - 2 Hours]
5 --> 8
6 --> 9[Task 9 - 5 Hours]
7 --> 9
8 --> 9
Predecessors in Partial Orders
if $R$ is a partial order on a set $A$ and $xRy, x\neq y$ we call $x$ a predecessor of $y$.
If $x$ is a predecessor of $y$ and there is no $z\in\{x,y\}$ for which $xRy$ and $zRy$, we call $x$ and immeditate predecessor of $y$.
graph LR
subgraph R
y -.-> z
z -.-> x
x --> y
end
In this graph if you can see no $z$ in-between $x$ and $y$ then $y$ is an immediate predecessor of $x$.
Integer Example
For the function $\leq$ on the set $\Bbb{Z}$ the immediate predecessor of a number $n$ is $n-1$.
graph LR
subgraph Z
1[n-1] --> 2[n]
end
Hasse Diagram
The Hasse Diagram of a partial order is a digraph. The vertices of the digraph are the elements of the partial order, and the edges of the digraph are given by the “immediate predecessor” relation.
This is an example for the bit vector representation of a set containing 3 elements. Each relation is a subset relation:
graph BT
0[0,0,0] --- 1[0,0,1]
0 --- 2[0,1,0]
0 --- 4[1,0,0]
1 --- 3[0,1,1]
1 --- 5[1,0,1]
2 --- 3
2 --- 6[1,1,0]
4 --- 5
4 --- 6
3 --- 7[1,1,1]
5 --- 7
6 --- 7
It is typical to assume that the arrow pointing upwards.
This diagram notation saves us from having to draw all the reflexive links and also all of the dependency links by just drawing the immediate dependency.
Total Orders
A binary relation $R$ on a set $A$ is a total order if it is a partial order such that any $x,y\in A,xRy$ or $yRx$.
This means that for any relation you can always compare them.
The Hasse diagram of a total order is a chain.
This means that there are no splits as splits mean that they aren’t comparable.
Examples
- The relation $\leq$ on the set $\Bbb{R}$ of real numbers.
- The usual lexicographical ordering on words in a dictionary.
- The relation “is a divisor of” is not a total order.
All the relations we have been looking at so far have been binary relations however this can be generalised for greater numbered relations.
$n$-ary Relations
The Cartesian product $A_1\times A_2\times \ldots \times A_n$ of sets $A_1,A_2,\ldots,A_n$ is defined by:
\[\begin{aligned}
A_1\times A_2\times \ldots \times A_n=&\\
\{(a_1,\ldots,a_n)\ \vert\ a_1\in A_1,\ldots,a_n\in A_n\}&
\end{aligned}\]
Here $(a_1,\ldots,a_n)=(b_1,\ldots,b_n$ if and only if $a_i=b_i$ for all $1\leq i\leq n$.
An $n$-ary relation is a subset of $A_1\times\ldots A_n$
Databases and Relations
A database table $\approx$ relation.
Table 1 $\text{Students}$
| Student_name |
ID_number |
Major |
GPA |
| Ackermann |
231455 |
Computer Science |
3.88 |
| Adams |
888323 |
Physics |
3.45 |
| Chou |
102147 |
Computer Science |
3.49 |
| Goodfriend |
453876 |
Mathematics |
3.45 |
| Rao |
678543 |
Mathematics |
3.9 |
| Stevens |
786576 |
Psychology |
2.99 |
This student table is a subset of the Cartesian product of four sets containing names, ID numbers, subject and GPA. We can then write these properties in tuples in the subset: $\text{Students}=\{\text{(Ackerman, 231455,}$$\text{ Computer Science, 3.88)}\ldots\}$.
Unary Relations
Unary relation are just subsets of a set.
Example
The unary relation $\text{EvenPositiveIntegers}$ on the set $\Bbb{Z^+}$ of positive integers is:
\[\{x\in\Bbb{Z^+}\ \vert\ x \text{ is even}\}\]
This shows that a unary relation is just a list of items in a set the satisfy a property.
This topic is very similar to the subjects covered in COMP111’s propositional logic. As result I will only be noting down significant differences.
Logic is concerned with the truth a falsity of statements. The question is when does a statement follow from a set of statements.
Propositional Logic
Propositional logic is logic which only concerns itself with whether something is true or false. Other languages differ themselves as they deal with uncertainties.
A proposition is a statement that can either be true or false. A statement like $4+5$ is not a proposition as it doesn’t give a true or false answer.
Compound Propositions
More complex propositions are formed using logical connectives (also called Boolean connectives).
The basic connectives are:
- $\neg$: Negation (read “not”).
- $\wedge$: Conjunction (read “and”).
- $\vee$: Disjunction (read “or”).
- These are the scientific names and they make a difference between the english and mathematical words.
- $\Rightarrow$: Implication (read “if…then”).
- In other schools this may be written as $\rightarrow$ or as $\subseteq$.
- $\Leftrightarrow$: Equivalence (read “if, and only if,”).
- Similar to 4. the notation is not as set as 1,2 and 3. This may be written as $\leftrightarrow$ or $\equiv$.
Propositional formed using these logical connectives are called compound propositions; otherwise atomic propositions.
- A propositional formula is either an atom ic or compound proposition.
This lecture is very similar to COMP111’s truth values lecture. View that lecture for all truth tables.
Truth Values
Interpretations are a way of assigning values to propositions which may vary depending on the situation or person who answers them.
An interpretation $I$ is a function which assigns to any atomic proposition $p_i$ a truth value:
\[I(p_i)\in \{0,1\}\]
- If $I(p_i)=1$, then $p_i$ is called true under the interpretation $I$.
- If $I(p_i)=0$, then $p_i$ is called false under the interpretation $I$.
Given an assignment $I$ we can compute the truth value of compute formulas step by step using so-called truth tables.
Implication
The implication $(P\Rightarrow Q)$ of $P$ and $Q$:
\(\text{If } P \text{ then } Q\)
Truth Table
| $P$ |
$Q$ |
$(P\Rightarrow Q)$ |
| 1 |
1 |
1 |
| 1 |
0 |
0 |
| 0 |
1 |
1 |
| 0 |
0 |
1 |
Consider this table with the proposition $P$ being a promise. If you don’t make a promise but you fulfil it anyway then you aren’t breaking that promise.
Another example would be the following statement:
- If a number is divisible by 6 then it is divisible by 3.
- If it is not divisible by 6 but still divides by 3, this does not invalidate the proposition.
Semantic Consequence
Suppose $\Gamma$ is a finite set of formulas and $P$ is a formula. Then $P$ follows from $\Gamma$ (is a semantic consequence of $\Gamma$) if the following implication holds for every interpretation $I$:
\[\text{If } I(Q)=1\text{ for all } Q\in \Gamma,\text{then } I(P)=1\]
This is denoted by:
\[\Gamma \models P\]
Logical Puzzles
An island has two kinds of inhabitants, knights, who always tell the truth, and knaves, who always lie.
You go to the island and meet $A$ and $B$.
- $A$ says, “$B$ is a knight.”
- $B$ says, “The two of us are opposite types.”
What are $A$ and $B$?
We can prove this in a proof by cases or, as the two people have a binary type you can model this question as below.
$p$: “$A$ is a knight”; and $q$: “$B$ is a knight”
Options for $A$
- $p$ is true $p\Rightarrow q$
- $p$ is false $\neg p\Rightarrow \neg q$
Options for $B$
- $q$ is true $q\Rightarrow \neg p$
- $q$ is false $\neg q\Rightarrow \neg p$
Here we are summarising the two statements as logical propositions.
Truth Table
| $p$ |
$q$ |
$\neg p$ |
$\neg q$ |
$p\Rightarrow q$ |
$\neg p\Rightarrow \neg q$ |
$q\Rightarrow \neg p$ |
$\neg q\Rightarrow \neg p$ |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
$\wedge$-ing together all the answers shows that the correct answer is $p=0,q=0$. This means that $A$ is a knave and $B$ is a knave.
Say that the implications in the truth table are numbered, $\{1,2,3,4\}$. We can then rewrite this table as the following statement:
\[\{1,2,3,4\}\models \neg p \wedge \neg q\]
Examples
-
Show $\{(p_1\wedge p_2)\}\models (p_1\vee p_2)$.
| $p_1$ |
$p_2$ |
$(p_1\wedge p_2)$ |
$(p_1\vee p_2)$ |
| 1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
The top line represents $(p_1\vee p_2)$ which we can see as $p_1=1, p_2=1$. As the proposition and the result hold true in this case then the statement is correct.
-
Show $\{p_1\}\not\models p_2$
| $p_1$ |
$p_2$ |
| 1 |
1 |
| 1 |
0 |
| 0 |
1 |
| 0 |
0 |
From this table we can see that the statement is correct as when $p_1=1, p_2=0$.
Logic and Proof Principles
Modus Ponens
Direct proof corresponds to the following semantic consequence:
\[\{P,(P\Rightarrow Q)\}\models Q\]
Reducto ad Absurdum
Proof by contradiction corresponds to:
\[\{(\neg P\Rightarrow\bot)\}\models P\]
where $\bot$ is a special proposition, which is false under ever interpretation. $\bot=a\wedge\neg a$.
Modus Tollens
Another look at proof by contradiction:
\[\{(P\Rightarrow Q),\neg Q\}\models\neg P\]
Case Analysis
\[\{(P\Rightarrow Q),(R\Rightarrow Q),(P\vee R)\}\models Q\]
Proof Theory
We have studies proof as carefully reasoned arguments to convince a sceptical listener that a given statement is true. These are called social proofs.
Proof theory is a branch of mathematical logic dealing with proofs as a mathematical objects:
- Strings of symbols.
- Rules for manipulation.
- Mathematics becomes a game played with strings of symbols.
- Can be read and interpreted by computers.
This is to say that in prof theory we make statements that computers are able to solve by putting them in a very structured language. This language can then be solved by Boolean logic.
Digital Logic Circuits
In Series
This circuit produces similar results to an AND gate:

In Parallel
This circuit produces similar results to an OR gate:

Modern computers use logic gates.
Basic Logic Gates
AND Gate

| $P$ |
$Q$ |
$R$ |
| 1 |
1 |
1 |
| 1 |
0 |
0 |
| 0 |
1 |
0 |
| 0 |
0 |
0 |
OR Gate

| $P$ |
$Q$ |
$R$ |
| 1 |
1 |
1 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
NOT Gate

Rules for a Combinatorial Circuit
- Never combine two input wires.
- A single input wire can be split partway and used as input for two separate gates.
- An output wire can be used as input.
- No output of a gate can eventually feed back into that gate.
There are some additional examples in the video that I haven’t covered here as they are very logical.
If you want to and together multiple values you can either use a multi-input package or string together a multi-gate package. Here are two equivalent diagrams:


Say you have the following table of inputs and outputs you want to have in a circuit:
| Input |
Input |
Input |
Output |
| P |
Q |
R |
S |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
- View all the lines where the output is given.
- From these construct a formulas with all inputs where the output is satisfied AND-ed together.
- OR all these atoms together.
This will give you:
\[(P\wedge Q \wedge R)\vee(P\wedge\neg Q\wedge R)\vee(P\wedge Q\wedge\neg R)\]
This is the disjunctive normal form (DNF).
You can then convert this into a circuit diagram:

This formula and diagram can be simplified to give the following:
\[P\wedge (Q\vee R)\]

You can see this from investigating the table.
Circuit Equivalence
Two circuits are equivalent if they produce the same output given the same input.
Logical Equivalence
Two formulas $P$ and $Q$ are called equivalent if they have the same truth value under every possible interpretation. In other words, $P$ and $Q$Q are equivalent if $I(p)=I(Q)$ for every interpretation $I$. This is denoted by:
\[P\equiv Q\]
Theorem
The relation $\equiv$ is an equivalence relation on $\mathcal{P}$.
Proof
- $\equiv$ is reflexive, since, trivially, $I(P)=I(P)$ for every interpretation $I$.
- $\equiv$ is transitive, since $P\equiv Q$ and $Q\equiv R$ implies $P\equiv R$.
- $\equiv$ is symmetric, since $P\equiv Q$ implies $Q\equiv P$.
Useful Equivalences
Associative Laws
\(\begin{aligned}
(P\vee (Q\vee R))&\equiv((P\vee Q)\vee R)\\
(P\wedge (Q\wedge R))&\equiv((P\wedge Q)\wedge R)
\end{aligned}\)
Commutative Laws
\(\begin{aligned}
(P\vee Q)&\equiv (Q\vee P)\\
(P\wedge Q)&\equiv (Q\wedge P)
\end{aligned}\)
Identity Laws
\(\begin{aligned}
(P\vee\bot)&\equiv P\\
(P\vee\top)&\equiv \top\\
(P\wedge\top)&\equiv P\\
(P\wedge\bot)&\equiv \bot
\end{aligned}\)
Distributive Laws
\(\begin{aligned}
(P\wedge(Q\vee R))&\equiv((P\wedge Q)\vee(P\wedge R))\\
(P\vee(Q\wedge R))&\equiv((P\vee Q)\wedge(P\vee R))
\end{aligned}\)
Complement Laws
\(\begin{aligned}
P\vee\neg P&\equiv\top\\
\neg\top&\equiv\bot\\
\neg\neg P&\equiv P\\
P\wedge\neg P&\equiv\bot\\
\neg\bot&\equiv\top
\end{aligned}\)
De Morgan’s Laws
\(\begin{aligned}
\neg(P\vee Q)&\equiv(\neg P\wedge \neg Q)\\
\neg(P\wedge Q)&\equiv(\neg P\vee \neg Q)
\end{aligned}\)
Sequential Circuits
Rules for a Sequential Circuit
- Never combine two input wires.
- A singe input wire can be split partway and used as input for two separate gates.
- An output wire can be used as input.
- An output of a gate can eventually feed back into that gate.
The only difference here between a combinatorial and a sequential circuit is the final rule.
What Happens Here?
-
For the following circuit we know that the input would be $P$, making the output $\neg P$.

This would not make sense as the wire says that they are equivalent.
In real life this circuit would oscillate due to the time delay in switching. This would continue until it depleted the power in the circuit.
-

This circuit will stay high or low depending on the initial value of the circuit.
This is the same as this circuit with NOR gates:

For this circuit one of the inputs are fixed at zero. This follows on to the next subtopic.
Set/Reset Flip-Flop Circuit
This circuit is also known as a latch.

The two input signals are:
This needs constant refreshing as the output will go when the power is removed.
Boolean Functions
Below are two tables containing all the possible outputs and possible inputs of the two variables $P$ and $Q$. We should be able to deduce the function of $P$ and $Q$ that gives the results:
| $P$ |
$Q$ |
$\bot$ |
$P\wedge Q$ |
$\neg(P\Rightarrow Q)$ |
$P$ |
$\neg(Q\Rightarrow P)$ |
$Q$ |
$\neg(P\equiv Q)$ |
$P\vee Q$ |
| 1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| $P$ |
$Q$ |
$\neg(P\vee Q)$ |
$P\equiv Q$ |
$\neg Q$ |
$Q\Rightarrow P$ |
$\neg P$ |
$P\Rightarrow Q$ |
$\neg(P\wedge Q)$ |
$\top$ |
| 1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Logic Gates
Universality of NAND and NOR
Both the NAND and NOR gates can be used in place of any other gate. They also have their own symbols:
- NAND (Sheffer Stroke)
- $P\vert Q=\neg(P\wedge Q)$
- NOR (Pierce Arrow)
- $P\downarrow Q=\neg(P\vee Q)$
The universality means that they can be used as all gates:
By using a single gate we can drive cost down through economy of scale.
Number Systems
To indicate that a number of from a particular base system then use a subscript to denote this:
- $4268_{10}$
- $1100\ 0111_2$
In a positional system you should multiply each digit by its place value:
- $4268_{10}=4\times 10^3+2\times 10^2+6\times 10^1 +$$\ 8\times 10^0$
Convert Decimal to Binary
The rule is to repeatedly divide by 2, writing down the remainder from each stage from right to left.
Example
- $\frac{533}{2}=266r1$
- $\frac{266}{2}=133r0$
- $\frac{133}{2}=66r1$
- $\frac{66}{2}=33r0$
- $\frac{33}{2}=16r1$
- $\frac{16}{2}=8r0$
- $\frac{8}{2}=4r0$
- $\frac{4}{2}=2r0$
- $\frac{2}{2}=1r0$
- $\frac{1}{2}=0r1$
You will read this from bottom to top.
Therefore:
\[533_{10}=1000010101_2\]
Alternative Method
If you know the powers of 2, continually subtract largest power value from the number.
This is the method that I usually use. The other method is best suited to a programmatic implementation.
Binary Addition
This topic was covered in this lecture. View the video for the full example.
Half Adder
This adder can add one bit only.
| $P$ |
$Q$ |
Carry |
Sum |
| 1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |

Full Adder
This adder can be linked together to add any number of bits together.
| $P$ |
$Q$ |
$C_{\text{in}}$ |
$C_{\text{out}}$ |
$S$ |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
0 |

Black Box Notation
To save drawing out all of the gates every time you can draw the diagram as a package. There is also a symbol for an adder:

4-bit Adder
To complete the following calculation:
\[\begin{array}{ccccc}
&a_3&a_2&a_1&a_0\\
+&b_3&b_2&b_1&b_0\\
\hline
c&s_3&s_2&s_1&s_0
\end{array}\]
You would use the following circuit:

If the carry out from this is non-zero then there has been an overflow and the value is larger than you can provide space for.
This is an example of a combinatorial circuit.
Computer Representation of Negative Integers
Typically a fixed number of bits is used to represent integers:
- Unsigned integers can take up all space.
- Signed Integers
- Leading Sign
- Uses the first bit to denote being negative.
- This can store negative zero which is not desired.
- Two’s Complement
-
Given a positive integer $a$, the two’s complement of $a$, relative to a fixed bit length $n$, is the binary representation of:
\[2^n-a\]
-
You can view this as flipping the bits.
Two’s Complement
The two’s complement of $a=3$ is:
\[2^4-3=13=1101_2=-3_{10}\]
The bonus of two’s complement is that $-1_{10}=1111_2$ will roll over to 0 when you add 1 to it. This also means that there is no two’s complement of zero as it is an overflow. This is good as we don’t want negative zero.
Properties
- Positive numbers start with 0, negative numbers start with 1.
- 0 is always represented as a string of zeros.
- -1 is always represented as a string of ones.
- The number range is split unevenly between $+ve$ and $-ve$ numbers (If 0 is positive then is is even).
- The range of numbers we can represent in $n$ bits is $-2^{n-1}$ to $2^{n-1}-1$.
Addition & Subtraction
You can add any negative number in order to take it. Generally any carry that goes off the end can be ignored.
Overflow
If Both inputs to an addition have the same sign, and the output sign is different, an overflow has occurred.
Overflow cannot occur if inputs have opposite sign.
Two’s Complement & Bit Negation
Take the example of $n=4$:
- $s^4-a=((2^4-1)-a)+1$
- The binary representation of $(2^4-1)$ is $1111_2$.
- Subtracting a 4-bit number $a$ from $1111_2$ just switches all the 0’s in $a$ to 1’s and all the 1’s to 0’s.
- So, to compute the two’s complement of $a$, flip the bits and add 1.
Converting to Decimal
To find the decimal representation of the integer with a given two’s complement:
- Fint the two’s complement of the given two’s complement.
- Write the decimal equivalent of the result.
4-bit Subtractor
The following diagram is an implementation of $a-b$ as the sum of $a$ and the two’s complement of $b$.

This flips the bits of $b$ and adds one via the carry in.
A more automated approach would be the following:

The XOR gates flip the bits when Subtract is high. Additionally, when Subtract is high 1 is added to the carry in.
Floating Point Numbers
It is not always possible to express numbers in integer form.
Real, or floating point numbers are used in the computer when:
When using floating point numbers the number is writen like in scientific notation.
Binary Fractions
Fractions can be represented in base 2:
\[\begin{aligned}
10.01_2&=1\times 2^1+0\times2^0+0\times2^{-1}+1\times2^{-2}\\
&=1\times2+0+0+1\times0.25\\
&=2.25_{10}
\end{aligned}\]
This gives a scientific representation of $10.10_2=1.001\times2^1$
In binary, for any non-zero number the leading digit is always 1.
To represent a number in scientific notation:
- The sign of the number.
- The magnitude of the number, known as the matissa or significand.
- The sign of the exponent
- the magnitude of the exponent.
Example - 1 Byte
\[S\ EE\ MMMMM\]
- $S$ is the sign of the number.
- $EE$ are the two characters encoding the exponent.
- $MMMMM$ are five characters for the mantissa.
IEEE 754
IEEE standard for floating point arithmetic. This is implemented in many hardware units and stipulates the computer representations of numbers:
- 16 bit half precision numbers.
- 5 for exponent, 11 for mantissa.
- 32 bit single precision numbers.
- 8 for exponent, 24 for mantissa.
- 64 bit double precision numbers.
- 11 for exponent, 53 for mantissa.
- 128 bit quadrouple precision numbers.
- 15 for exponent, 113 for mantissa.
- 16256bit octouple precision numbers.
- 19 for exponent, 237 for mantissa.
As numbers are not stored as surds, small rounding error can accumulate if there isn’t enough precision.
Developing Ideas
Chairs
All the chairs in a room are labelled with a single digit followed by a lower-case letter. What is the largest number of differently numbered chairs?
Generally, to do this you would multiply the base of each digit together.
Bits
How many different bit strings of length 8 are there?
You can model this as a binary search tree of length 8 as each bit can either be zero of one.
graph TD
a[ ] -->|1| b[ ]
a[ ] -->|0| c[ ]
b[ ] -->|1| d[ ]
b[ ] -->|0| e[ ]
c[ ] -->|1| f[ ]
c[ ] -->|0| g[ ]
You can see that the the number of options are given by the base:
\[2\times 2\times 2\times 2\times 2\times 2\times 2\times 2=2^8\]
You can visualise this as the number of options doubling at each branch.
Students
How many was are there to select 3 students for a prospectus photo (order matters) from a group of 5?
You can view this as having 5 possibilities to fill position one, four for position two, and 3 for position three.
By using the same tree philosophy from the last algorithm you can work this out by doing $5\times 4\times 3$.
The Product Rule
If there is a sequence of $k$ events with $n_1,\ldots,n_k$ possible outcomes, then the total number of outcomes for the sequence of $k$ events is:
\[n_1\times n_2\times\ldots\times n_k\]
Example 1
How many distinct car licence plates are there consisting of six character, the first three of which are letters and the last three of which are digits?
From this you would calculate:
\[26\times26\times26\times10\times10\times10\]
Example 2
How many ways are there to select a male and female student for a prospectus photograph (order matters) from a group of 2 male and 3 female students?
For this example you could start with the female on the left or the right. This will result in $3\times2$ and $2\times3$. You would then add these together to get:
\[2\times2\times3\]
This is an example of two disjoint events.
Disjoint Events
Two events are said to be disjoint (or mutually exclusive) if they can’t occur simultaneously.
If you have 3 pair of blue jeans and 2 pairs of black jeans, then there are $3+2=5$ different pairs of jeans for you to wear.
The Sum Rule
If $A$ and $B$ are disjoint events and there are $n_1$ possible outcomes for event $A$ and $n_2$ possible outcomes for event $B$ then there are $n_1+n_2$ possible outcomes for the event either $A$ or $B$.
Examples
-
How many three-digit numbers begin with 3 or 4.
Here you can separate the events as numbers beginning with 3 or 4. From this you would get:
\[10\times10+10\times10\]
Or you could say that the first value could take two values (3 or 4) giving:
\[2\times10\times10\]
-
I wish to take two pieces of fruit with me for lunch. I have three banana, four apples and two pears. How many ways can I select two pieces fo fruit of different type? (order doesn’t matter)
From this you can generate three disjoint groups:
- Apple, Banana
- Apple, Pear
- Banana, Pear
In each of these groups you have a number of fruits:
- Apple, Banana $=4\times3$
- Apple, Pear $=4\times2$
- Banana, Pear $=3\times2$
This would then give:
\[12 + 8 + 6 = 26\]
Set-Theoretic Interpretation
If $A$ and $B$ are disjoint sets (that is, $A\cap B=\emptyset$) then $\vert A\cup B\vert=\vert A\vert+\vert B\vert$.
Any sequence of $k$ events can be regarded as an element of the Cartesian product $A_1\times\ldots\times A_k$. This set has size $\vert A_1\vert\times\ldots\times\vert A_k\vert$.
Examples
-
A computer password is a sting of 8 characters, where each character is an uppercase letter or a digit. Each password must contain at least one digit. How many different passwords are there?
For this we first consider the number of passwords, ignoring the at least one digit constraint. Then we can consider the passwords that are not allowed and subtract them from this set.
The cardinality of each character in the good and bad set would be 36. This would give $36^8$ total passwords.
The cardinality of the passwords in the bad set would be $26^8$. This is the set of passwords containing only letters.
This would give a total of:
\[36^8-26^8\]
-
How many different 8 character passwords can be obtained by combining a 3 letter word, a 4 letter word and a digit. There are 1015 3 letter and 4030 4 letter words.
Here you have 3 elements with cardinality $\{1015,4030,10\}$ that could be in 6 permutations. From this you would calculate:
\[1015\times4030\times10\times6\]
This is significantly smaller than the last example.
The Subtraction Rule
If there are $n_1$ possible outcomes of event $A$, $n_2$ possible outcomes for event $B$ and $n_3$ of these outcomes are shared between $A$ and $B$ then there are:
\[n_1+n_2-n_3\]
possible outcomes for the event $A$ OR $B$.
Example
How many bit strings of length 8 start with 1 or finish with 00?
Here you are completing a logical OR. You add the two combinations together and subtract the intersect.
\[2^7+2^6-2^5\]
The Division Rule
Given $n$ possible outcomes if:
- Some of the $n$ outcomes are the same.
- Every group of indistinguishable outcomes contains exactly $d$ elements.
There are $\frac{n}{d}$ different outcomes.
Example
How many ways are there to select 2 representatives from a group of 5 students?
By taking into account ordering you would count every pair twice. Here what we really want is a distinct subset of two students.
Summary
The four decomposition rules are:
- The product rule
- The sum rule
- The subtraction rule
- The division rule
- For indistinguishable outcomes.
Sums and Products of a Sequence
Given a sequence of numbers:
\[a_1,a_2,\ldots,a_m,\ldots,a_n\]
we can use the notation:
- $\sum^n_{i=m}a_i$ to represent $a_m+\ldots+a_n$.
- $\prod^n_{i=m}a_i$ to represent $a_m\times\ldots\times a_n$.
Following from this you could combine indexes to make multiple iteration:
\[\sum^5_{i=1}\sum^5_{j=i}(i+5)\]
Here you would apply the sum using $j$ for each sum using $i$. The lower bound for the inner sum would increase every time to match the incrementing $i$.
Special Case $m=n$
\(\sum^n_{i=m}=a_m\)
Here you would just state the element at that index in the list.
Sums and Products Over Sets of Indices
Let $f:D\rightarrow\Bbb R$ be a function with some domain $D$. Then for $S\subseteq D$:
Example
Suppose that the domain $D=\{a,b,c,d\}$. Additionally there is a function $f:D\rightarrow\Bbb R$
\[\begin{aligned}
f(a)&=0&f(b)&=1\\
f(c)&=0.3&f(d)&=-1
\end{aligned}\]
To find the sum of all the elements in $D$ with the function applied to them would be:
\[\sum_{i\in D}f(i)=0+1+.3-1=.3\]
The same applies to products.
The Factorial Function
The product $\prod^n_{i=1}i$ comes up so often that is has a name. it is called $n$ factorial and is written as $n!$.
As $i=1$ then $0!=1$.
Permutations
A permutation of a set is just an ordering of its elements.
By the product rule the number of permutations of an $n$-element set is $n!$.
- This is because there are $n$ choices for the first element, then $n-1$ choices for the 2nd element, then $n-2$ choices for the 3rd element and so on.
- Therefore the number of permutations of a list of 3 elements would be $3!=6$
$k$-Permutations
A selection of $k$ distinct elements of a set, where order matters is called a $k$-permutation of the set.
The number $k$-permutations of an $n$-element set is:
\[\begin{aligned}
P(n,k)&=n\times(n-1)\times\ldots\times(n-(k-1))\\
&=\frac{n!}{(n-k)!}
\end{aligned}\]
From the example last lecture, the number of combinations of three elements from a set of five elements where order matters is $P(5,3)=$ $5\times4\times3$.
Notable Example
I have a jar with 3 different sweet. Three children come in, and each take one. How many different outcomes are there?
\[P(3,3)=3\times2\times1=\frac{3!}{0!}=6\]
This is an example of why $0!$ is 1.
Additionally, if the factorial is too large to calculate, you can cancel out values in the numerator and denominator to get a more manageable number.
Counting $k$-Combinations
A size-$k$ subset is called a $k$-combination.
The number of $k$-combinations of a set of size $n$ is:
\[C(n,k)=\frac{n!}{(n-k)!k!}\]
Proof
- The number of $k$-permutations of the set is $P(n,k)=\frac{n!}{(n-k)!}$.
- A $k$-permutation is an ordering of $k$ distinct elements of the set.
- Each size-$k$ subset has $k!$ orderings, so it corresponds to $P(k,k)=k!$ of the $k$ permutations.
- By the division rule, $C(n,k)=\frac{P(n,k)}{P(k,k)}=\frac{n!}{(n-k)!k!}$.
This is to say that by dividing out the repeat values we are left with just distinct values.
Combination Examples
The number of size 1 subsets of $\{1,2,3,4,5\}$ is 5. This is also the number of size 4 subsets of the set.
Any opposite subset sizes sample complements of each other and are therefore the same size.
Twelve people, including Mary and Peter, are candidates to serve on a committee of five. How many different committees are possible?
There are:
\[C(12,5)=\frac{12!}{(12-5)!5!}=792\]
This is as a result of choosing combinations of 5 people form a set of 12 people.
Of These How Many
- Contain both Mary and Peter?
\(C(10,3)=120\)
In this case we disregard them and adjust the samples and sample size accordingly.
- Contain neither Mary and Peter?
\(C(10,5)=252\)
In this case we select 5 members from the set without them.
-
Contain either Mary or Peter (but not both)?
\(2\times C(10,4)=420\)
This is because we have two possible cases for Mary and Peter which have combinations $C(10,4)=210$.
Binomial Coefficients
The quantity $C(n,k)$, which gives the number of $k$-combinations of a set of size $n$, is called a binomial coefficient.
It is also written as:
\[{n\choose k}=\frac{n!}{(n-k)!k!}\]
This notation is preferred.
Binomial Theorem
For every natural number $n$:
\[(a+b)^n=\sum^n_{k=0}{n\choose k}a^kb^{n-k}\]
This is the sum of a generic binomial expansion.
Pascal’s Triangle
The choose notation directly relates to pascals triangle. For a generic expansion the row is the power and the value is the coefficient of the related position in the expansion.
Binomial Coefficient Identity
\[{n+1\choose r+1}={n\choose r}+{n\choose r+1}\]
Proof:
- ${n+1\choose r+1}$ is the number of ways to choose a subset of size $r+1$ form a st of size $n+1$.
- Suppose the set is $\{x_1,x_2,\ldots,x_{n+1}\}$.
- How many subsets include $x_{x+1}$? We just choose a size-$r$ subset from $\{x_1,x_2,\ldots,x_{n+1}\}$, so there are $n\choose r+1$ ways to do it.
- These outcomes are disjoint, so the total number of subsets is the sum of $n\choose r$ and $n\choose r+1$.
Counting and Probabilities
Counting also helps us to answer questions like:
- What are the odds of winning the National Lottery?
- What payoffs should you expect?
- What is more likely in poker, full house or 4-of-a-kind?



