An algorithm is a sequence of steps for performing a task in a finite amount of time.
The following properties of algorithms are in order of importance:
- Running Time (Time Complexity)
- Memory Usage (Space Complexity)
- Optimality of the output solution.
Experimental Analysis of Algorithms
This is the collection of empirical data at runtime.
The running time depends on the size and instance of the input and the algorithm used where:
- Size - The number of inputs in a list.
- Instance - The state of the inputs:
- Optimal and worst-case scenarios.
Drawbacks of Experimental Analysis
- Experiments are performed on a limited set of test inputs.
- Requires all tests to be performed using same hardware and software.
- Requires implementation and execution of algorithm.
Theoretical Analysis
Benefits over Experimental Analysis
- Can take all possible inputs into account.
- Can compare efficiency of many algorithms, independent of hardware/software environment.
- Involves studying high-level descriptions of algorithms:
Language to Describe Algorithms
We use pseudo-code as a high-level description language for algorithms like so:
Minimum-Element(A)
/** Find the minimum of elements in the array A. **/
min ← A[1]
for j ← 2 to length[A]
do
/* Compare element A[j] to current min
and store it if it’s smaller. */
if A[j] < min
then min ← A[j]
return min
This course will not use a strict method for defining pseudo-code. It should however be clear as to not be misinterpreted.
Computational Model
This course will use a Random Access Machine (RAM) model that is comprised of the following components:
- CPU
- RAM
- A bank of memory cells, each of wuich can store a number, character, or address.
Primitive operations like:
- Single Addition
- Multiplication
- Comparison
take constant time to run.
This is not true in physical CPUs, it is just an assumption.
Measuring Running Time
To measure running time we count the primitive operations. We can do this using the previous example:
Minimum-Element(A)
min ← A[1] # O(1)
for j ← 2 to length[A] # O(n - 1)
do
# Compare element A[j] to current min
# and store it if it’s smaller.
if A[j] < min # O(n - 1)
then min ← A[j] # O(n - 1)
return min # O(n)
This sums to give:
\[3(n-1)+2\]
Characterising Running Time
An algorithm may run faster on some inputs compared to others.
- Average-Case Complexity - Running time as an average taken over all inputs of the same size.
- Worst-Case Complexity - Running time as the maximum taken over all inputs of the same size.
Usually, we’re most interested in worst-case complexity.
This type of notation allows for the characterisation of the main factors affecting running time.
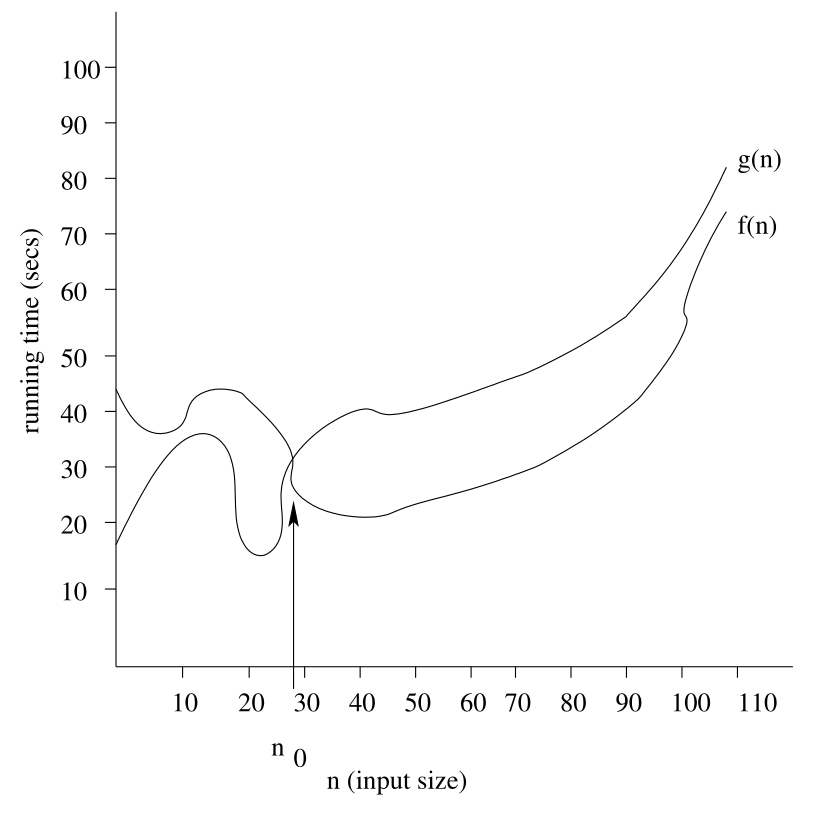
Big-O Notation
Given two positive functions (algorithms) $f(n)$ and $g(n)$, defined on non-negative integers, we say:
\[f(n) \text{ is } O(g(n))\]
or equivalently:
\[f(n) \in O(g(n))\]
if there are constants $c$ and $n_0$ such that:
\[\forall n\geq n_0, f(n)\leq c\cdot g(n)\]
We want to see what it takes to make $g$ be greater than $f$.
This can also be represented in the following graph:
Big-O Example
Consider the example of:
\[7n - 4\in O(n)\]
To validate this we need to find constants $c$ and $n_0$ such that:
\[\forall n\geq n_0, 7n-4\leq cn\]
We could choose the values:
In order to satisfy the inequality we could have chosen any real numbeer $c\geq7$ and any integer $n_0\geq1$.
There are additional big-O examples in the slides.
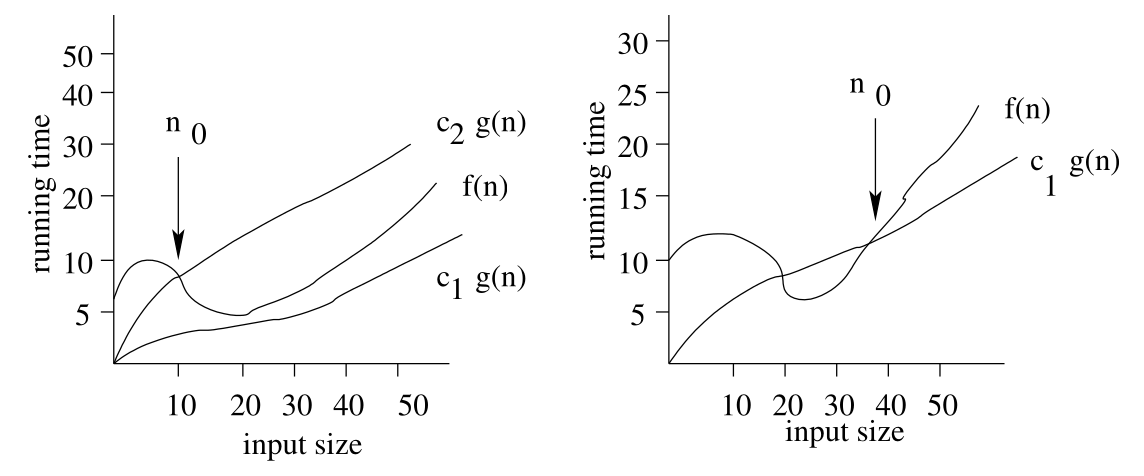
$\Omega(n)$ & $\Theta(n)$ Notation
-
We say that $f(n)$ is $\Omega(g(n))$ (big-Omega) if there are real constants $c$ and $n_0$ such that:
\[\forall n\geq n_0 f(n)\geq cg(n)\]
-
We say the $f(n)$ is $\Theta(g(n))$ (big-Theta) if $f(n)$ is $\Omega(g(n))$ and $f(n)$ is also $O(g(n))$.
You can see and example of this in the following graphs:
Renter’s Dilemma
Consider that to rent a film it costs $x$ but to buy it, it costs $10\times x$. We want to decide when would be the best time to buy the film.
Online vs. Offline Algorithms
- Online Setting - Requests arrive sequentially and upon arrival they must be dealt with immediately.
- Offline Setting - The entire sequence of events are given and the optimal solution must be chosen.
Competitive Analysis
This is the process of comparing a given online algorithm $A$ to an optimal offline algorithm $OPT$.
We can say that, given a sequence of requests $R=(r_1,r_2,\ldots,r_n)$, the costs of using either algorithm are calculated like so:
- cost($OPT,R$)
- cost($A, R$)
Algorithm $A$ is c-competitive, for some $c\geq1$, for $R$ if:
\[\text{cost}(A,r)\leq c\cdot \text{cost}(OPT,R)+b\]
for some constant $b>0$.
If $A$ is c-competitive for ever sequence $R$, then we say that $A$ is c-competitive:
- $c$ is the competitive ratio.
If $b=0$, then $A$ is strictly c-competitive.
Renters Dilemma Example
Consider the following strategy for an online algorithm:
You rent the film every time you want to watch it.
- This will cause you to spend $n\times x$ which could be up to $\frac {n\times x} {10}$ more pounds than is optimal.
A more optimal solution would be to rent 10 times and then buy the film.
- In this case you would spend at most 2 times more than an offline strategy. You can call this 2-competitive.
You can find an analysis of this at slide 50.
This course will use the following types of proof:
I won’t cover these here, as they have been covered before, but there are additional examples in the slides.
Linked Lists & Arrays
This lecture started by covering arrays and linked lists. There are several lectures on linked lists below:
Dictonaries & Sorted Tables
We can store data in a key-value dictionary store like so: Collections (Generics, Stacks, Hash Maps)
If a dictionary is ordered, we can create a vector to store the values sorted by their key.
Binary Search
This method has been covered before in the following lectures:
We can calculate the time complexity of the recursive algorithms using the following cases:
\[T(n)=
\begin{cases}
b & \text{if } n < 2\\
T(\frac n 2) +b & \text{otherwise}
\end{cases}\]
To find the total running time then we need to find how many halves it takes to get to one item remaining. This give the order of:
\[O(\log n)\]
We can compare the time complexity of a linked list and sorted array:
| Method |
Linked List |
Lookup Table |
findElement |
$O(n)$ |
$O(\log n)$ |
insertItem - Having located the item. |
$O(1)$ |
|
removeElement |
$O(n)$ |
$O(n)$ |
closestKeyBefore |
$O(n)$ |
$O(\log n)$ |
We can use a binary search tree to take advantage of the search capabilities of an array while maintaining the insertion speed on a linked list.
Trees
Rooted Trees
These are a standard tree data-structure which has a root node with no parent.
Binary Tree
This is a rooted tree with at most two children on each node. They can be represented by the following data-structure:
graph TD
subgraph node
lp[Parent Link] --- value
value --- ln[Left Link]
value --- rn[Right Link]
end
Depth of Node in a Tree
The depth of a node, $v$, is the number of ancestors of $v$, excluding $v$ itself. This can be computed using the following function:
$\text{depth}(T,v)$
if T.isRoot(v) then
return 0
else
return 1 + Depth(T, T.parent(v))
Height of a Tree
the height of a tree is equal to the maximum depth of an external node in it. This function computes the height of the subtree rooted at $v$.
$\text{height}(T,v)$
if isExternal(v) then
return 0
else
h = 0
for each w in T.children(v) do
h = max(h, height(T, W))
done
return 1 + h
Traversal of Trees
Traversal of trees has been covered in this lecture:
Binary Search Trees
We can apply this traversal to binary search trees. We have seen this before in the following lecture:
Searching in a BST
Here is a recursive searching method:
- Input - A key $k$ and a node $v$ of a binary search tree.
- Output - A node $w$ in the subtree $T(v)$, either $w$ is an internal node with key $k$ or $w$ is an external node where the key $k$ would belong if it existed.
$\text{treeSearch}(k,v)$
if isExternal(v) then
return v
if k = key (v)
then return v
elseif k < key(v) then
return treeSearch(k, T.leftChild(v))
else
return treeSearch(k, T.rightChild(v))
AVL Trees
You can view interactive examples of AVL trees at: https://www.cs.usfca.edu/∼galles/visualization/AVLtree.html.
This is a type of tree which upholds a height-balance property. This rule says that the heights of the children of a node can differ by at most 1.
This means that the height of an AVL tree storing $n$ items is:
$O(\log n)$
This also means that:
- A search in an AVL tree can be performed in $O(\log n)$ time.
- Insertions an removals take more time as the height-balance property must be maintained.
AVL Tree Insertion
- Complete an insertion as for BST trees.
- Re-balance the tree from the bottom up to maintain the height-balance property.
There are several “rotations” that can be performed to re-balance a tree after insertion. They are mostly intuitive and are similar to the following:
-
The tree is unbalanced as the children of the root have heights with difference more than one:
graph TD
a["(4)"] --> T0["T0 (1)"] & b["(3)"]
b --> T1["T1(1)"] & c["(2)"]
c --> T2["T2 (1)"] & T3["T3 (1)"]
$T_0$ and so on are arbitrary sub-trees. The height of a specific node is in brackets ().
-
This can be re-arranged in the following way to be balanced:
graph TD
a[ ] --> b[ ] & c[ ]
b --> T0 & T1
c --> T2 & T3
There are additional examples starting at slide 46 of the lectures and in the second tutorial.
AVL Tree Deletion
- Complete the deletion like in a BST.
- Re-balance the tree from the bottom-up.
Consider that the tree is left in the following state after deletion:
graph TD
44 --> 17
17 --> a[ ] & b[ ]
44 --> 62
62 --> 50 & 78
50 --> 48 & 54
48 --> c[ ] & d[ ]
54 --> e[ ] & f[ ]
78 --> g[ ] & 82
82 --> h[ ] & i[ ]
subgraph deleted
32 --> oa[ ] & ob[ ]
end
We can make the largest child of the root the new root and then rearrange the rest of the graph:
graph TD
44 --> 17
17 --> a[ ] & b[ ]
44 --> 50
62 --> 44 & 78
50 --> 48 & 54
48 --> c[ ] & d[ ]
54 --> e[ ] & f[ ]
78 --> g[ ] & 82
82 --> h[ ] & i[ ]
Nodes with smaller values should be on the left in these graphs.
All operations (search, insertion and removal) on an AVL tree with $n$ elements can be performed in:
\[O(\log n)\]
(2, 4) Trees
This may have identical behaviour to a B-Tree with max degree 4. In which case, you can view interactive visualisations here: https://www.cs.usfca.edu/~galles/visualization/BTree.html.
Every node in a (2, 4) tree has:
- At least 2 children.
- At most 4 children.
Each internal node (not leaves) contain between 1 and 3 values:
graph TD
12 --> a[5 10] & 15
a --> b[3 4] & c[6 7 8] & 11
15 --> d[13 4] & 17
This creates a tree in which all leaf nodes have the same depth at $\Theta(\log n)$.
(2, 4) Trees Search
Searching for a key $k$ in a (2, 4) tree $T$ is done via tracing the path in $T$ starting at the root in a top-down manner:
Visiting a node $v$ we compare $k$ with keys ($k_i$) stores at $v$:
- If $k=k_i$ the search is completed.
- If $k_i\leq k \leq k_{i+1}$, the $i+1^{\text{th}}$ subtree of $v$ is searched recursively.
(2, 4) Trees Insertion
Insertion of $k$ into a (2, 4) tree $T$ begins with a search for an internal node with the lowest level that could accommodate $k$ without violating the range.
This action may overflow the node-size of a node $v$ acquiring the new key $k$. We can use the split operation to fix this:
-
There is an overflowing tree to split:
graph TD
a[h1 h1] --> w1 & b[k1 k2 k3 k4] & w3
b --> v1 & v2 & v3 & v4 & v5
-
We move the middle value up to the next level and split the original node with values ordered appropriately:
graph TD
a[h1 k3 h2] --> w1 & b[k1 k2] & c[k4] & w3
b --> v1 & v2 & v3
c --> v4 & v5
(2, 4) Trees Deletion
- Deletion of a key $k$ from a (2, 4) tree $T$ begins with a search for node $v$ possessing key $k_i=k$.
- Key $k_i$ is replaced by the largest key in the $i^{\text{th}}$ consecutive subtree of $v$.
- A bottom-up mechanism, based on transfer and fusion operations, fixes any underflow.
| Operation |
Time |
| Split, Transfer & Fusion |
$O(1)$ |
| Search, Insertion & Removal |
$O(\log n)$ |
Priority Queues
A priority queue is a container of elements, each having an associated key:
- The key determines the priority used in picking elements to be removed.
A priority queue has these fundamental methods:
insertItem(k, e) - Insert an element $e$ having key $k$ into the PQ.removeMin() - Remove the minimum element.minElement() - Return the minimum element.minKey() - Return the key of the minimum element.
Priority Queue Sorting (Heap Sort)
We can use a PQ to perform sorting on a set $C$ using the following steps:
- Put elements of $C$ into an initial empty priority queue, $P$, by a series of $n$
insertItem operations.
- Extract the elements from $P$ in non-decreasing order using a series of $n$
removeMin operations.
We can use the following pseudo-code to complete this:
while c /= empty
do
e = C.removeFirst()
P.insertItem(e, e)
while P /= empty
do
e = P.removeMin()
C.insertLast(e)
This operation takes:
\[O(n\log n)\]
Heaps
A heap is an implementation of a PQ:
- A heap allows insertions and deletions to be performed in logarithmic time.
- The elements and their keys are stored in an almost complete binary tree.
- Every level of the binary tree, except for the last, will have the maximum number of children.
graph TD
heap --- 4
4 --> 5 & 6
5 --> 15 & 9
6 --> 7 & 20
15 --> 16 & 25
9 --> 14 & 152[15]
7 --> 11 & 8
8 --- last
In a heap $T$, for every node $v$ (excluding the root) they key at $v$ is greater than, or equal to, the key stored in its parent.
Insertion in Heaps
- Add the new element to the bottom of the tree in the position of the first unused, or empty, child.
- If required, this element bubbles (swaps) its ways up the heap, until the heap order property is restored.
Deletion in a Heap
- Remove the element at the root of the tree.
- Move the last element to the root position.
- Swap the element down the tree if the order is incorrect.
The time for heap operations are presented below:
| Operation |
Time |
size, isEmpty |
$O(1)$ |
minElement, minKey |
$O(1)$ |
insertItem |
$O\log n$ |
removeItem |
$O\log n$ |
Merge Sort
This is a method of applying divide and conquer to sorting. It uses the following steps:
- If input sequence $S$ has 0 or 1 elements, then return $S$. Otherwise, split $S$ into two sequences $S_1$ and $S_2$, each containing $\frac 1 2$ of the elements in $S$ - Divide
- Recursively sort $S_1$ and $S_2$ - Recur
- Put the elements back into $S$ by merging the sorted sequences $S_1$ and $S_2$ into a single sorted sequence. - Conquer
Merge Sort Analysis
Merging two sorted sequences $S_1$ and $S_2$ takes $O(n_1+n_2)$ time, where $n_1$ is the size of $S_1$ and $n_2$ is the size of $S_2$.
Merge sort runs in:
\[O(n\log n)\]
time in the worst case.
We can justify this as:
- During every recursive step, dividing each sub-list takes time at most $O(n)$ time.
- Merging all the lists in each level takes at most $O(n)$ times at well.
As we recurse at most $O(\log n)$ times this gives the $O(n\log n)$ running time.
Counting Inversions
Consider that you have a list of movies that you have rated out of 10. To give a user recommendations we may want to compare our ratings to others who have rated the moves in a similar way.
We can also say, which of the following lists have the closest rankings:
\[2, 7, 10, 4, 6, 1, 3, 9, 8, 5\\
8, 9, 10, 1, 3, 4, 2, 5, 6, 7\]
to your ranking:
\[1, 2, 3, 4, 5, 6, 7, 8, 9, 10\]
Method for Counting Inversions
To count the number of inversions, for each element that is in an index lower than what it should be - count all the following numbers that are lower than it
The following example has one inversion:
\[2, 1, 3, 4, 5\]
as 2 is in the wrong position and only 1 is less than it and later in the list.
In this example there are seven inversions:
\[5,4,1,2,3\]
as $5>4,5>1,5>2,5>3$ and $4>1,4>2,4>3$.
Counting Inversions - Divide & Conquer
The standard approach for counting inversions takes:
\[\Omega(n^2)\]
we can speed this up by using the following method.
- Divide the permutation into two fairly equal parts.
- Sort each sub-list and merge them into a single sorted list. Then count the inversions again.
This is a modified merge sort.
Divide & Conquer Pseudo-code
countInversions(L)
if L has one element in it then
there are no inversions, so return(0, L)
else
divide the list into two halves
A contains the first n/2 elements
B contains the last n/2 elements
(k_A, A) = countInversions(A)
(k_B, B) = countInversions(B)
(k, L) = mergeAndCount(A, B)
return (k_A + k_B + k, L)
mergeAndCount(A, B)
CurrentA = 0
CurrentB = 0
Count = 0
L = []
while both lists (A and B) are non-empty
let a_i and b_j denote the elements pointed to by CurrentA and CurrentB
append the smaller of a_i and b_j to L
if b_j is the smaller element then
increase Count by the number of elements remaining in A
advance the Current pointer of the appropriate list
Once one of A and B is empty, append the remaining elements to L
return(Count, L)
This method has a time of:
\[O(n\log n)\]
Quick Sort
- Divide if $\vert S\vert>1$, select a pivot element $x$ in $S$ and create three sequences:
- $L$ stores elements in $S$ that are less than $x$.
- $E$ stores elements in $S$ that are equal to $x$.
- $G$ stores elements in $S$ that are greater than $x$.
- Recursively sort the sequences $L$ and $G$.
- Put the sorted elements from $L$, $E$ and $G$ together to form a sorted list.
The worst case running time is:
\[O(n^2)\]
however we can improve this, by using a random pivot to:
\[O(n\log n)\]
We can use this to select a good pivot that balances the binary tree that is created.
- A good pivot has at least $\frac 1 4$ of the whole list on both sides of the pivot.
- The probability of choosing a good pivot is $\frac 1 2$ as there are $\frac n 2$ good pivots.
- As a result we can expect to get a good pivot in two repeats.
- As the list will have at most $\frac 3 4$ of the list on either side of the pivot, there are at most $\log_{\frac 4 3} n$ levels when using good pivots.
- Hence, the expected length of each path will be $2\log_{\frac4 3}n$
Bucket Sort
Bucket sort is not based on comparisons but on using keys as indices of a bucket array.
-
Initially all items of the input sequence $S$ are moved to appropriate buckets.
An item with key $k$ is moved to bucket $B[k]$.
-
Then move all items back into $S$ according to their order of appearance in consecutive buckets.
Bucket Sort Pseudo-code
- Input - A sequence $S$ of items with integer keys indexed from 0.
- Output - Sequence $S$ sorted in non-decreasing order of keys.
for each item x in S
do
let k be key of item x
B[k] = remove(x,S)
for i = 0 to N - 1
do
for each item x in sequence B[i]
do S = remove(x, B[i])
Radix Sort
This is an type of bucket sort that was originally used by punched card sorting machines. It can be used to sort ordered pairs into lexicographic order, where each coordinate lies in the range of integers.
In general, we can use radix sorting to sort ordered d-tuples into lexicographic ordering.
A d-tuple is a tuple with at most $d$ digits.
If words have uneven length then no letter is less than any letter: $\text{ab} < \text{abc}$.
Radix Sort Method
Sort a single column of digits, from the least to most significant digit, making $d$ passes over the data to do so.
$d$ is the number of place-values in your largest number.
We should stably sort each column. This means that if there is a tie then the original order is preserved.
| Original List |
$d=1$ |
$d=2$ |
$d=3$ |
| 159 |
742 |
108 |
108 |
| 496 |
125 |
125 |
125 |
| 375 |
496 |
742 |
159 |
| 125 |
896 |
357 |
357 |
| 896 |
357 |
159 |
496 |
| 742 |
108 |
496 |
742 |
| 108 |
159 |
896 |
896 |
Radix Sort Time Analysis
For a list with $n$ items and the largest number being $d$ digits long radix sort will take:
\[O(d(n+N))\]
where $N$ is $\max(n,d)$.
Running Time of Divide & Conquer
We can use a recurrence relation to analyse the running time where:
- $T(n)$ denotes the running time on an input of size $n$.
We can then extend this with a case statement that relates $T(n)$ to values of the function $T$ for problem sizes smaller than $n$.
For example, the running time of merge sort can be written in this form:
\[T(n) =
\begin{cases}
c & \text{if }n<2\\
2T(\frac n 2)+cn &\text{otherwise}
\end{cases}\]
$c$ is a small constant that represents how much work is done for the each iteration.
Substitution Method
One way to solve a divide and conquer recurrence equation is to use the iterative substitution method. For the previous example
\[T(n) =
\begin{cases}
c & \text{if }n<2\\
2T(\frac n 2)+cn &\text{otherwise}
\end{cases}\]
Assuming that $n$ is a power of 2 we get:
\[\begin{aligned}
T(n) &= 2\left(2T(\frac n {2^2}) +c(\frac n 2)\right)+cn\\
&=2^2 T(\frac n {2^2}) + 2cn
\end{aligned}\]
For $i=\log_2n$, we get:
\[\begin{aligned}
T(n) &= 2^{\log_2n}\times c + cn\log_2n\\
&=cn + cn \log_2n\\
&= \Theta(n\log n)
\end{aligned}\]
General Method
We can also use this method which may be simpler: Divide & Conquer Tutorial - Running Time Alternate Method
We can use a more general method that takes the form:
\[T(n)=
\begin{cases}
c & \text{if } n\leq d\\
aT(\frac n b)+f(n) & \text{if } n>d
\end{cases}\]
with some constants $a,b,c$ and $d$, and some function $f(n)$.
$f(n)$ accounts for the recursive preparation time and the time taken to merge.
We can “unwind” this recurrence relation like so:
\[\begin{aligned}
T(n) &= aT(\frac n b) +f(n)\\
&= a \left(aT(\frac n {b^2}) +f(\frac n b)\right)+f(n)\\
&= a^2T(\frac n {b^2}) +af(\frac n b)+f(n)\\
&= a^3T(\frac n {b^3}) + a^2f(\frac n {b^2}) +af(\frac n b)+f(n)\\
&= \ldots\\
&=a^{\log_bn}T(1)\sum^{\log_bn-1}_{j=0}a^jf(\frac n {b^i})\\
&=n^{\log_ba}T(1)\sum^{\log_bn-1}_{j=0}a^jf(\frac n {b^i})\\
\end{aligned}\]
Once we have the time in this form we can make one of the following conclusions:
- If $f(n)$ is smaller than $n^{\log_ba}$, then the first term is going to dominate the summation, and we will have $T(n)=\Theta(n^{\log_ba})$.
- If there is a constant $k\geq 0$ such that $f(n)$ is $\Omega(n^{\log_ba}\log^kn)$, then $T(n)$ is $\Theta(n^{log_ba}\log^{k+1}n)$.
- If $n^{\log_ba}$ is smaller than $f(n)$, then the summation will dominate this expression and we will have $T(n)=\Theta\left(f(n)\right)$
There is a nice example of using the master method starting at slide 13.
Cammy has a video example at: https://youtu.be/Sn3D9_TmyWw.
Running Time Alternate Method
Instead of using the method stated here we can use this easier method instead for:
\[T(n) = aT\left(\frac n b\right) + f(n)\]
where:
\[f(n) = O(n^d)\]
We can then use the following cases:
\[T(n) =
\begin{cases}
O(n^d) & \text{if } d>\log_ba\\
O(n^d\log_bn) &\text{if } d=log_ba\\
O(n^{log_ba}) &\text{if } d<log_ba
\end{cases}\]
Fast Multiplication of Integers
A logical multiplication algorithm will take $\Theta(n^2)$ time to complete. We can do better by doing a fast multiplication.
- Consider that we have two numbers, $I$ and $J$, to multiply together.
- Pad the numbers with zeros, at the beginning, so that the length of each number $n$ is a power of two.
-
Split the numbers into high and low bits like so:
\[\begin{aligned}
I &= I_h2^{\frac n 2}+I_l\\
J &= J_h2^{\frac n 2}+j_l
\end{aligned}\]
We multiply the high bit by an integer power of two in order to left shift the high bit back into place. This is important as each left shift only takes $O(1)$ time.
-
Compute recursively the product of the above equations like so:
\[\begin{aligned}
I \times J &= (I_h2^{\frac n 2}+I_l)(J_h2^{\frac n 2}+j_l)\\
&= I_hJ_h2^n+\left((I_h-I_l)(J_l-J_h)+I_jJ_h+I_lJ_l\right)2^{\frac n 2} + I_lJ_l\\
&= I_hJ_h2^n+I_lJ_h2^{\frac n 2}+I_hJ_l2^{\frac n 2}+I_lJ_l
\end{aligned}\]
Each multiplication that isn’t a bit-shift, should be put into the final equation again.
Time Complexity of Fast Multiplication
The recurrence relation describing this operation is:
\[T(n)=3T\left(\frac n 2\right)+cn\]
using the master method we can calculate that:
\[\Theta\left(n^{\log_23}\right)=O\left(n^{1.585}\right)\]
Fast Matrix Multiplication
For the following calculation:
\[\pmatrix{A & B\\C & D}\pmatrix{E & F\\G & H}=\pmatrix{I&J\\K&L}\]
we can use the Strassen algorithm to find the solution:
-
Find the following seven matrix products:
\[\begin{aligned}
S_1 &= A(F-H)\\
S_2 &= (A+B)H\\
S_3 &= (C+D)E\\
S_4 &= D(G-E)\\
S_5 &= (A + D)(E+H)\\
S_6 &= (B-D)(G+H)\\
S_7 &= (C-A)(E+F)
\end{aligned}\]
This is one less multiplication than you would usually do when calculating a matrix product.
-
Find $I, J, K$ & $L$ using the following:
\[\begin{aligned}
I &= S_4 + S_5 +S_6 - S_2\\\
J &= S_1 + S_2\\
K &= S_3 + S_4\\
L &= S_1 + S_5 + S_7 - S_3
\end{aligned}\]
Time Complexity of Fast Matrix Multiplication
The recurrence relation describing this operation is:
\[T(n) = 7T\left(\frac n 2\right) + bn^2\]
Using the master method we can find that this operation takes:
\[O\left(n^{\log_27}\right)=O\left(n^{2.808}\right)\]
This is faster than the usual time of $O\left(n^3\right)$.
The greedy method solves optimisation problems by going through a sequence of feasible choices.
The sequence starts from a well-understood configuration and then iteratively makes the decision that seems best from all those that are currently possible.
Problems that have a greedy solution possess the greedy-choice property.
Fractional Knapsack Problem
This is a variation of the knapsack problem where we are able to take arbitrary fractions of each item. The problem is formally defined like so:
Let $S$ be a set of $n$ items, where each item $i$ has a positive benefit $b_i$ and a positive weight $w_i$. Additionally, we are allowed to take arbitrary fractions $x_i$ of each item such that $0\leq x_i\leq w_i$.
Goal - Find the maximum benefit subset that does not exceeds the total weight $W$.
The total benefit of the items taken is determined by the sum:
\[\sum_{i\in S}b_i\left(\frac{x_i}{w_i}\right)\]
Fractional Knapsack Method
The general method takes the following form:
-
Compute the value index for each item $i$ defined by:
\[v_i=\frac{b_i}{w_i}\]
-
Select the items to include in the knapsack, starting with the highest value index.
We can implement this in the following pseudo-code:
fractionalKnapsack(S, W)
for i = 1 to |S| do
xi = 0
vi = bi / wi
insert(vi, i) into heap H // max value at root
w = o
while w < W do
Remove the max value from H
a = min(wi, W - w)
xi = a
w = w + a
- Input - Set of $S$ items, item $i$ has weight $w_i$ and benefit $b_i$; maximum total weight $W$.
- Output - Amount $x_i$ of each item to maximise the total benefit.
Time Complexity of Fractional Knapsack Problem
- Using a heap, with the maximum at the root, we can compute the value indices and build the heap in $O(n\log n)$ time.
- Then, each greedy choice, which removes an item with the greatest remain value index, requires $O(\log n)$ time.
The {0, 1} - Knapsack Problem
This is the same knapsack problem that was discussed in COMP208 - Greedy Algorithm - 1 - Knapsack Problem where you cannot take fractions of items.
As discussed in that lecture, the greedy method will not find an optimal solution to this problem. To solve this we can use a dynamic programming approach instead.
Interval Scheduling
Consider that we have a set of tasks to execute on a machine. We want to select a set of task to maximise the number of tasks that are executed on the machine.
Given a set $T$ of $n$ tasks, where each task has a start time $s_i$ and end time $f_i$. Two tasks $i$ and $j$ are non-conflicting if:
\[f_i\leq s_j \text{ or } f_j\leq s_i\]
A suitable method to find such a schedule would be to select non-conflicting tasks in order of their finish times.
This allows us to free up the machine as soon as possible for further activities.
We can do this with the following pseudo-code:
intervalSchedule(T)
A = []
while T != []
do
Remove the task t with the earliest completion time.
Add t to A
Delete all tasks from T that conflict with t
Return the set A as the set of scheduled tasks
- Input - A set $T$ of tasks with start times and end times.
- Output - A maximum-size subset $A$ of non-conflicting tasks.
This algorithm can run in:
\[O(n\log n)\]
where the main amount of time is sorting the tasks by their completion times.
Multiple Machine Task Scheduling
Consider that instead of one machine, we have a set of machines. We want to execute the tasks using as few machines as possible. We can use the following greedy algorithm to compute the schedules:
Consider the set of tasks ordered by their start times. For each task $i$, if we have a machine that is non-conflicting, then we schedule the task to that machine. Otherwise, we allocate a new machine.
We can do this with the following pseudo-code:
taskSchedule(T)
m = 0
while T != []
do
removeMin(T)
if every machine j with no conflicts
then schedule(i,j)
else
m = m + 1
schedule(i, m)
- Input - A set $T$ of tasks with start times and end times.
- Output - A non-conflicting schedule of the $T$ tasks.
This algorithm also takes the following amount of time:
\[O(n\log n)\]
There is a proof of this algorithm starting from slide 28 of the lecture.
Clustering
This is the process of classifying objects based on their distance.
Consider that we want to categorise $n$ objects into $k$ (non-empty) clusters. We want each cluster $C_1, \ldots, C_k$ to be maximally spaced apart.
In order to do this, we can consider our objects as points that need to be joined together into several graphs. We can connect objects together, in order of their distance, until we have the same number of graphs as $k$.
We should connect objects in such a way that there are no cycles, similar to Kruskal’s algorithm.
This algorithm takes:
\[O(n^2\log n)\]
where the main bottleneck is to perform the sort of the pairwise distances.
There is a proof of this procedure starting from slide 40 of the lecture.
Dynamic programming is similar to divide-and-conquer however, recursive calls are replaced by looking up pre-computed values. We can use it to compute optimisation problems where a brute force search is infeasible.
A typical approach to solve a problem using dynamic programming is to first find a recursive solution to the problem:
-
Once this is found, we then try to determine a way to compute the solutions to the sub-problems in a bottom up approach.
This avoids recomputing the same solutions many times.
Fibonacci Numbers
We have covered a dynamic programming approach to solving this problem in the following lecture:
{0, 1} Knapsack Problem
Previously we have covered sub-optimal solutions to this problem using a greedy approach. By using dynamic programming we can make an optimal solution that doesn’t have exponential time.
See Greedy Algorithm Applications - Knapsack, Scheduling, Clustering to revise the notation used.
{0, 1} Knapsack Problem Solution
Let $S_k={1,2,\ldots,k}$ denote the set containing the first $k$ items and define $S_0=\emptyset$.
Let $B[k,w]$ be the maximum total benefit obtained using a subset of $S_k$, and having total weight at most $w$.
Then we define $B[0,w]=0$ for each $w\leq W_\max$ and:
\[B[k,w]=
\begin{cases}
B[k-1,w]&\text{if } w<w_k\\
\max\{B[k-1,w],b_k+B[k-1,w-w_k]\} & \text{otherwise}
\end{cases}\]
Our solution is then $B[n,W_\max]$.
To make our solution as easy as possible to find, we will compute these values from the bottom-up:
- First we compute $B[1,w]$ for each $w\leq W_\max$ and so on.
We can implement this in the following pseudo-code:
01knapSack(S,W)
for w = 0 to W
do
B[0, w] = 0
for k = 1 to n
do
for w = 0 to wk - 1
do
B[k, w] = B[k - 1, w]
for w = W downto wk
do
if B[k - 1, w - wk] + bk > B[k - 1, w] then
B[k, w] = B[k - 1, w - wk] + bk
else
B[k, w] = B[k - 1, w]
- Input - Set $S$ of $n$ items with weights $w_i$, benefits $b_i$ and total weight $W$.
- Output - A subset $T$ of $S$ with weight at most $W$.
{0, 1} Knapsack Problem Time Complexity
The running time of 01knapSack is dominated by the two nested for loops, where the outer loop iterates $n$ times and the inner loop $W$ times.
Therefore, this algorithms finds the highest benefit subset of $S$ with total weight at most $W$ in:
\[O(nW)\]
Weighted Interval Scheduling
This is similar to interval scheduling however, now the tasks have a value $v_i$.
The goal is to schedule a subset of non-conflicting intervals that have a maximal total value.
We cannot achieve this goal using a greedy approach.
Weighted Interval Scheduling Solution
A divide and conquer approach would look like the following:
- Sort the intervals in terms of their finishing time.
- Define $p(j)$ to be the interval $i$ where:
- $i$ and $j$ are non-conflicting.
- $i$ has the largest finish time whilst occuring before $j$ ($f_i\leq s_j$).
$p(j)=0$ if there is no such $i$.
- Define $S_j$ to be the optimal solution and $\text{Opt}(j)$ to be the value of $S_j$.
-
If $j\in S_j$ then:
\[\text{Opt}(j) = v_j + \text{Opt}(p(j))\]
-
If $j\notin S_j$ then:
\[\text{Opt} = \text{Opt}(j - 1)\]
-
Therefore:
\[\text{Opt}(j) = \max\{v_j+\text{Opt}(p(j)), \text{Opt}(j-1)\}\]
To avoid an exponential time solution, we solve all values $\text{Opt}(1), \ldots,\text{Opt}(n)$ in advance of the next step.
-
We can then derive $S_j$ recursively depending on the value above:
\[S_j=
\begin{cases}
S_{p(j)} \cup \{j\} & \text{if } \text{Opt}(j) = v_j + \text{Opt}(p(j))\\
S_{j-1} & \text{if } \text{Opt} = \text{Opt}(j - 1)
\end{cases}\]
For the definition of a graph see the lectures:
An undirected graph $G$ is simple if there is at most one edge between each pair of vertices $u$ and $v$.
A digraph is simple if there is at most one directed edge from $u$ to $v$ for every pair of distinct vertices $u$ and $v$.
Therefore, for a graph $G$ with $n$ vertices and $m$ edges:
-
If $G$ is undirected, then:
\[m\leq \frac{n(n-1)}2\]
-
If $G$ is directed, then:
\[m\leq n(n-1)\]
Describing Walks & Paths
A walk is a sequence of alternating vertices and edges, starting at a vertex and ending at a vertex.
A path is a walk where each vertex in the walk is distinct.
We can describe this walk with the following syntax:
graph LR
A -->|e2| B -->|e13| D -->|e10| C
\[A, e_2, B, e_{13}, D, e_{10}, C\]
If this is part of a simple graph then this walk could be written as:
\[A, B, D, C\]
Terminology
- A subgraph of a graph G is a graph $H$ whose vertices and edges are subsets of the vertices and edges of $G$.
- A spanning subgraph of $G$ is a subgraph of $G$ that contains all the vertices of $G$.
- A graph is connected if, for any two distinct vertices, there is a path between them.
- If a graph $G$ is not connected, its maximal connected subgraphs are called the connected components of $G$.
- A forest is a graph with no cycles.
- A tree is a connected forest (a connected graph with no cycles).
- A spanning tree of a graph is a spanning subgraph that is a free tree (no root node).
Counting Edges
Let $G$ be an undirected graph with $n$ vertices and $m$ edges. We have the following observations:
- If $G$ is connected then $m\geq n-1$.
- If $G$ is a tree then $m=n-1$
- If $G$ is a forest then $m\leq n-1$
Representations of Graphs
We have covered many representations of graphs in previous lectures:
Graph Search Methods
We have covered various graph search methods before:
Single-Source Shortest Paths
We have covered this before in:
Dijkstra’s Algorithm
We have covered this before in:
We can use the following method to complete Dijkstra’s without path enumeration. For the following graph:
graph LR
d ---|2| e
d ---|4| c
e ---|4| f & b
c ---|1| e & b
c ---|4| f & a
b ---|1| f
f ---|1| a
we would represent the solution of completing Dijkstra’s from $d$ in the following table:
| a |
b |
c |
d |
e |
f |
Chosen |
| $\infty$ |
$\infty$ |
$\infty$ |
0 |
$\infty$ |
$\infty$ |
$\emptyset$ |
| $\infty$ |
$\infty$ |
4 |
0 |
2 |
$\infty$ |
${d}$ |
| $\infty$ |
6 |
3 |
0 |
2 |
6 |
${d,e}$ |
| 7 |
4 |
3 |
0 |
2 |
6 |
${c, d,e}$ |
| 7 |
4 |
3 |
0 |
2 |
5 |
${b, c, d,e}$ |
| 6 |
4 |
3 |
0 |
2 |
5 |
${b, c, d,e,f}$ |
| 6 |
4 |
3 |
0 |
2 |
5 |
${a,b, c, d,e,f}$ |
Dijkstra’s Algorithm Pseudo-Code
Dijkstra(G,v)
D[v] = 0
for each u != v do
D[u] = +INFTY
Let Q be a priority queue (heap) having all vertices of G using the D labels as keys.
while notEmpty(Q) do
u = removeMin(Q)
for each z s.t. (u, z) in E do
if D[u] + w({u, z}) < D[z]
then D[z] = D[u] + w({u, z})
key(z) = D[z] /* z might bubble up in the heap */
return D
Time Complexity of Dijkstra’s Algorithm
Let $G=(V, E)$ where $\vert V\vert=n$ and $\vert E\vert = m$.
Construction of the initial heap for the set of $n$ vertices takes $O(n\log n)$ time.
In each step of the while loop, getting the minimum entry from the heap requires $O(\log n)$ time (to update the heap), and then $O(\deg(u)\log n)$ time to perform the edge relaxation steps (and update the heap as necessary).
So the overall running time of the while loop is:
\[\sum_{u\in V(G)} (1+\deg(u))\log n = O((n+m)\log n)\]
Therefore Dijkstra’s algorithms solves SSSP in $O(m\log n)$ time as $n\leq m$ for connected graphs.
A flow network $G=(V,E)$ is a directed graph in which each edge $(u,v)\in E$ has a non-negative integer capacity $c(u,v)\geq 0$.
In a flow network there are two main vertices:
We assume that $s$ has no “in-edges” and that $t$ has no “out-edges”.
Each edge $(u,v)$ also has an associated flow value $f(u,v)$ which tells us how much flow has been sent along an edge. These values satisfy $0\leq f(u,v) \leq c(u,v)$.
$c$ is the capacity of a particular edge.
For every vertex other than $s$ and $t$, the amount of flow into the vertex must equal the amount of flow out of the vertex.
Maximum Flow Problem
In this type of problem we are expected to find a flow of maximum value from $s$ to $t$.
We might see a graph like so:
graph LR
s -->|3/7| v1
s -->|5/5| v3
s -->|6/6| v2
v1 -->|2/2| v4
v1 -->|1/1| v3
v3 -->|4/5| v4
v3 -->|2/3| t
v2 -->|0/3| v3
v2 -->|6/9| v5
v4 -->|6/6| t
v5 -->|6/8| t
Ford-Fulkerson Method
We can use this method to solve the maximum flow problem.
This algorithm searches for a flow-augmenting path from the source vertex $s$ to the sink vertex $t$. We then send as much flow as possible along the flow augmenting path, whilst obeying the capacity constraints of each edge.
The maximum flow we can send along the path is limited by the minimum of $c(u,v)$ and $f(u,v)$ of an edge on this path.
Formally:
- Start with $f(u,v) = 0$ for all $u, v\in V$.
-
At each iteration, we increase flow by finding an augmenting path from $s$ to $t$ along which we can push more flow.
We consider the residual network when we search for augmenting paths.
- This process is repeated until no more augmenting paths can be found.
The max-flow min-cut theorem proves that this process yields a maximum flow.
We can also write this method in the following pseudo code:
FFMethod(Graph $G$, source $s$, sink $t$)
f = 0
while augmenting path, P exists (in the residual network)
do augment flow along P
f = f + new flow
update residual network
return f
Ford-Fulkerson Time Complexity
Let $\lvert f^*\rvert$ denote the value of a maximum flow $f^*$ in a network with $n$ vertices and $m$ edges.
Finding an augmenting path in the residual network can be done using a DFS or BFS algorithm. These run in time:
\[O(n+m) = O(m)\]
Each augmentation increases the flow by at lease one unit (using the fact that the capacities are integers), so there are at most $\lvert f^*\rvert$ augmentation steps. This gives a time complexity of:
\[O(\lvert f^*\rvert m)\]
This isn’t ideal, as a poor choice of augmenting paths can result in a large time bound.
Residual Networks
A residual network shows additional flow that can occur across an existing network.
Consider that we have the following network:
graph LR
s -->|3/3| v
s -->|0/2| w
v -->|0/2| t
v -->|3/5| w
w -->|3/3| t
this will produce the following residual network:
flowchart LR
s -->|2| w
v -->|3| s
v -->|2| t
w -->|3| v
v -->|2| w
t -->|3| w
Forward flow is reversed, while any residual capacity stays the same.
We formally define the edges like so, where $G$ is the flow network and $G_f$ is the residual network:
-
Forwards Edges
For any edge $(u,v)$ in $G$ for which $f(u,v)<c(u,v)$, there is an edge $(u,v)$ in $G_f$.
The residual capacity $\Delta_f(u,v)$ of $(u,v)$ in $G_f$ is defined as $\Delta_f(u,v)=c(u,v)-f(u,v)$.
-
Backwards Edges
For any edge $(u,v)$ in $G$ for which $f(u,v)>0$, there is an edge $(v,u)$ in $G_f$.
The residual capacity $\Delta_f(v,u)$ of $(v,u)$ in $G_f$ is defined as $\Delta_f(v,u)=f(u,v)$.
Augmenting Paths
Given a flow network $G=(V,E)$ and a flow $f$, an augmenting path $P$ is a directed path from $s$ to $t$ in the residual network $G_f$.
An augmenting path is a path form the source to the sink in which we can send more net flow
Updating Flow
Once an augmenting path $P$ has been identified, we need to update the flow.
The amount of flow that can be sent along an augmenting path $P$ is limited by the edge with the least residual capacity, defined by:
\[\Delta_f(P) = \min_{(u,v)\in P}\Delta_f(u,v)\]
once we have calculated the capacity of this edge then we can take the following steps to update the flow network $G$ from the residual network $G_f$:
-
If $(u,v)$ is a forwards edge we set:
\[f(u,v) = f(u,v) + \Delta_f(P)\]
-
If $(u,v)$ is a backwards edge we set:
\[f(v,u) = f(v,u) - \Delta_f(P)\]
This means we decrease the flow along the original edge in $G$.
- For all edges $e$ not in $P$, we make no change.
- Finally, we update the residual network to correspond to the new flow network.
Cuts in Networks
A cut is a line that crosses a set of edges. It splits the network into two sub-graphs, one that contains $s$ and one that contains $t$. We can call these sub-graphs $S$ and $T$.
graph LR
s -->|3/3| o
s -->|2/3| p
o -->|3/3| q
o -->|0/2| p
p -->|2/2| r
q -->|2/2| t
q -->|1/4| r
r -->|3/3| t
subgraph S
s
p
end
subgraph T
o
q
r
t
end
I’ll call flow from $S$ to $T$ forward and from $T$ to $S$ backward.
The net flow across a cut is the sum of the forward flow, take the backward flow:
\[f(S,T) = \sum_{u\in S, v\in T}f(u,v)-\sum_{u\in T, v\in S} f(u,v)\]
The capacity of a cut is the sum of the forward flow:
\[c(S,T) = \sum_{u\in S, v\in T}c(u,v)\]
Max-Flow Min-Cut Theorem
The maximum flow of a network is equal to the capacity of a minimum cut in the network.
A bipartite graph is a graph whose vertex stet can be partitioned into two sets $X$ and $Y$, such that every edge joins a vertex in $X$ to a vertex in $Y$:
graph LR
x1 ------ y1 & y2
x2 ------ y1 & y3 & y2
x3 ------ y2
x4 ------ y1 & y3 & y2
Matchings
This is where we use a subset of the edges to produce a graph where each vertex appears in at most one edge.
Generally we want to produce the largest matching, such as pairing people with ideal tasks, so that people are has happy as possible.
We can generate such a matching by posing this as a network flow problem. We can add a source $s$ connected to all $x$ vertices and a sink $t$ connected to all $y$ vertices. We weight all edges as one:
graph LR
s ----|1| x1 & x2 & x3 & x4
y1 & y2 & y3 ----|1| t
x1 -----|1| y1 & y2
x2 -----|1| y1 & y3 & y2
x3 -----|1| y2
x4 -----|1| y1 & y3 & y2
We can then calculate a maximal matching using a maximal flow algorithm such as Ford-Fulkerson.
Symmetric Key Cryptography
This topic has been covered before in:
One-Time Pad
This is one of the most secure ciphers known.
For this encryption scheme Alice and Bob share a random bit string $K$ that is as long as any message that are going to send.
This key $K$ is the symmetric key that is used for the encryption and decryption process.
Although is is very secure and fast to compute, Alice and Bob must share very long keys $K$ which are used only once. This gives a lot of overhead.
One-Time Pad Encryption
-
To encrypt the message $M$, Alice computes:
\[C=M\oplus K\]
$\oplus$ is the exclusive or (XOR) operation.
-
Alice then sends $C$ to Bob on any reliable communication channel. The communication is secure because $C$ is computationally indistinguishable from a random bit string.
This relies highly on the fact that $K$ was selected randomly.
One-Time Pad Decryption
Bob can easily decrypt the cipher-text $C$ to recover $M$ using the following:
\[\begin{aligned}
C\oplus K &=(M\oplus K)\oplus K\\
&= M\oplus (K\oplus K)\\
&= M\oplus 0\\
&= M
\end{aligned}\]
where 0 represents the all-zero string with the same length as $M$.
Number Theory
The following methods allow us to devise a solution for public key cryptography.
Divisibility
Given integers $a$ and $b$, we use the notation $a\vert b$ to denote that $b$ is a multiple of $a$.
If $a\vert b$ then there is another integer $k$ such that $b=a\times k$. We note the following properties about this divisibility relationship:
Theorem: Let $a,b,c$ be integers:
- If $a\vert b$ and $b\vert c$ then $a\vert c$ (transitivity).
- If $a\vert b$ and $a\vert c$ then $a\vert(i\times b +j\times c)$ for all integers $i$ and $j$.
- If $a\vert b$ and $b\vert a$ then either $a=b$ or $a=-b$.
Prime Numbers and Composite Numbers
Integers that are not prime are composite.
Theorem: Let $n>1$ be an integer. Then there is a unique set of prime numbers ${p_1, \ldots,p_k}$ and positive integers ${e_1,\ldots,e_k}$ such that:
\[n=p_1^{e_1}\times\ldots\times p_k^{e_k}\]
The product $p_1^{e_1}\times\ldots\times p_k^{e_k}$ is known as the prime decomposition of $n$. It is unique, up to the ordering of the primes in the factorisation.
Greatest Common Divisor
Let $a$ and $b$ denote positive integers. The greatest common dividor of $a$ and $b$, denoted $\text{gcd}(a,b)$, is the largest integers that divides both $a$ and $b$.
If $\text{gcd}(a,b)=1$, then we say that $a$ and $b$ are relatively prime.
The definition of the GCD can be extended like so:
- If $a>0$, then $\text{gcd}(a,0)=\text{gcd}(0,a)=a$.
- $\text{gcd}(a,b)=\text{gcd}(\lvert a\rvert,\lvert b\rvert)$ if $a$ and/or $b$ is negative.
- $\text{gcd}(0,0)$ is undefined as there is no largest integer that divides 0.
Theorem: If $d=\text{gcd}(a,b)$, then there exist integers $j$ and $k$ such that:
\[d=j\times a +k\times b\]
In other words, the greatest common divisor of $a$ and $b$ is expressible as a linear combination of $a$ and $b$:
| Function |
Expression |
| $\text{gcd}(56,24)=8$ |
$8=1\times 56 +(-2)\times(24)$ |
| $\text{gcd}(25,32)=1$ |
$1=5\times 25 +(-4)\times 31$ |
| $\text{gcd}(45,25)=5$ |
$5=(-1)\times 45 +2\times 25$ |
| $\text{gcd}(57,363)=3$ |
$3=57\times 51 +(-8)\times 363$ |
Modulo Operator
For $b>0$, the modulo operator, denoted by $a\mod b$, defines the remainder of $a$ when divided by $b$. That is $r=a\mod b$ means that:
\[r=a-\left\lfloor\frac a b\right\rfloor b\]
This means that $r$ is always an integer in the set ${0,1,\ldots,b-1}$ (even when $a$ is negative), and there is an integer $q$ such that:
\[a=q\times b +r\]
Congruences
$a$ is congruent to $b$ modulo $n$ if the following is true:
\[a \mod n = b\mod n\]
We can write this as:
\[a\equiv b\pmod n\]
In other words, if $a\equiv b \pmod n$, then $a-b=kn$ for some integer $k$. We can see this in the following example:
\[16\equiv 8\pmod2\]
as $16-8$ is a multiple of 2.
Euclid’s Algorithm
Euclid’s algorithm is a method to fine the greatest common divisor of two integers $a$ and $b$. This algorithm relies on the following property:
Theorem: Suppose $a\geq b>0$, then:
\[\text{gcd}(a,b) = \text{gcd}(b,a\mod b)\]
Euclid’s Algorithm Pseudo-Code
EuclidGCD(a, b)
Input: $a$ and $b$ are non-negative and not both zero.
Output: $\text{gcd}(a,b)$
while b != 0 do
(a, b) = (b, a mod b)
return a
If $b=0$, this routine will return the value of $a$. This is correct under our assumption that $a$ and $b$ are not both zero.
Euclid’s Algorithm Example
We can display this algorithm in a table:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| $a$ |
412 |
260 |
152 |
108 |
44 |
20 |
4 |
| $b$ |
260 |
152 |
108 |
44 |
20 |
4 |
0 |
hence $\text{gcd}(412, 260)=4$.
Euclid’s Algorithm Time Complexity
For $i>0$, let $a_i$ denote the first element of the ordered pair during the $i^\text{th}$ step in the while loop. The second argument is equal to $a_{a+1}$, so:
\[a_{i+2} = a_i\mod a_{i+1}\]
This implies that, after the first time through the loop, the sequence $a_i$ is strictly deceasing.
We can show that $a_{i+2}<\frac 1 2 \times a_i$. This lead the following result:
Theorem: Let $a,b$ be two positive integers. Euclid’s algorithm computes $\text{gcd}(a,b)$ by executing:
\[O(\log(\max(a,b)))\]
arithmetic operations.
Extended Euclidean Algorithm
If $d=\text{gcd}(a,b)$, there are integers $j$ and $k$ such that $d=j\times a + k\times b$.
We can modify Euclid’s algorithm to fine these numbers $j$ and $k$ wehile we compute $\text{gcd}(a,b). This is called the extended Euclidean algorithm.
Extended Euclidean Algorithm Pseudo-Code
ExtendedEuclidGCD(a, b)
Input: Non-negative integers $a$ and $b$ (not both zero).
Output: $d=\text{gcd}(a,b)$, integers $j,k$ where $d=j\times a+k\times b$.
if b = o then
return (a, 1, 0)
r = a mod b
q = floor(a / b) // Let q be the integers such that a = q * b + r
(d, j, k) = ExtendedEuclidGCD(b,r)
return (d, k, j - kq)
Extended Euclidean Algorithm Example
We can represent $\text{gcd}(412, 260)$ in the following table:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| $a$ |
412 |
260 |
152 |
108 |
44 |
20 |
4 |
| $b$ |
260 |
152 |
108 |
44 |
20 |
4 |
0 |
| $q=\left\lfloor\frac a b\right\rfloor$ |
1 |
1 |
1 |
2 |
2 |
5 |
* |
| $r = a\mod b $ |
152 |
108 |
44 |
20 |
4 |
0 |
* |
| $j$ |
12 |
-7 |
5 |
-2 |
1 |
0 |
1 |
| $k$ |
-19 |
12 |
-7 |
5 |
-2 |
1 |
0 |
Note that $a,b,q$ and $r$ are filled from left to right, while $j$ and $k$ are filled from right to left. This means that the final answer for $j$ and $k$ are in column 1.
This produces the result of:
\[12\times 412 + (-19)\times260=4\]
Public-Key Cryptography
A public-key cryptosystem consists of an encryption function $E$ and a decryption function $D$. For any message $M$, the following properties must hold:
-
Both E and D are easy to compute for the following:
\[D(E(M))=M\\
E(D(M))=M\]
- It is computationally infeasible to derive D from E.
-
The knowledge of the encryption method gives no information about the decryption scheme. Anybody can send a private message to the hold of the function $D$, but only that person knows how to decrypt it.
For this reason $E$ is referred to as a one-way, or trapdoor, function.
In this kind of encryption method $E$ is made public and $D$ is kept private.
-
The recipient of a message should be able to verify that it came from the sender, assuming that the sender is the only person who has a the private key.
This is referred to as digital signatures.
RSA
RSA Encryption
The main idea of the RSA method is as follows:
- Let $p$ and $q$ denotes two large distinct prime numbers.
- Let $n=p\times q$ and define $\phi(n) = (p-1)(q-1)$.
- We can then choose two numbers $e$ and $d$ such that:
- $1<e<\phi(n)$
- $e$ and $\phi(n)$ are relatively prime ($\text{gcd}(e,\phi(n))$)
-
$ed\equiv1(\mod\phi(n))$
We can use the Extended Eculidean algorithm to find $d$, given $e$.
Assume that we have a message to send. We can split this message up into block of at most $n$ characters. We can then encrypt these messages $M$ and concatenate them back together later.
\[0<M<n\]
The plain-text $M$ is encrypted using the public keys $e$ and $n$ by the following operation:
\[C = M^e\mod n\]
RSA Decryption
Decryption of the received cipher-text $C$ is handled by modular exponentiation:
\[M = C^d \mod n\]
This is correct as for every integer $0<x<n$ we have:
\[x^{ed}\equiv x(\mod n)\]
RSA Encryption Strength
Even knowing $e$ doesn’t allow us to figure out $d$, unless we know $\phi(n)$.
Most cryptographers believe that breaking RSA required the computation of $\phi(n)$, which in turn requires factoring $n$. Factoring has not been proven to be difficult but it can take a long time to solve.
As the ability to factor large numbers increases, we simple have to choose larger primes $p$ and $q$ so that $n=p\times q$ is outside of the current factoring capabilities.
RSA Time Complexity
Using fast exponentiation, the size of the operands is never more than $O(\log n )$ bits, and it takes $O(\log k)$ arithmetic operations to find $x^k\mod n$.
This leads to the following result:
Theorem: Let $n$ be the modulus of the RSA algorithm. Then RSA encryption, decryption, signature and verification each take $O(\log n)$ arithmetic operations per block.
Digital Signatures
RSA supports digital signatures. Suppose that Bob sends a message $M$ to Alice and that Alice wants to verify that it was Bob who sent it. Bob can create a signature using the decryption function applied to $M$:
\[S = M^d\mod n\]
Alice verifies the digital signature using the encryption function, by checking that:
\[M\equiv S^e(\mod n)\]
Since only Bob knows the decryption function, this will verify that it was indeed Bob who sent the message.
Any person can use the encryption function as well to reconstruct the message $M$, so this is not a method to secretly pass information from Bob to Alice.
Fast Exponentiation
A possible bottleneck in the RSA algorithm is computing expressions of the form:
\[x^k \mod n\]
The naive approach is to calculate $x^2\mod n$, then use that to get $x^3\mod n$ and so on.
We can do much better with an algorithm based on repeated squaring. For example, if we wanted to compute $x^{16}$, we could first find $x^2$ and keep squaring to get $x^{16}$
If we are performing modular exponentiation, like in RSA, after each step we can find $x^i\mod n$ to keep the results small (between 0 and $n-1$).
Fast Exponentiation Pseudo-Code
FastExponentation(x, k, n)
Input: Integers $x, k\geq 0$, and $n>0$
Output: $r=x^k\mod n$
r = 1
t = x
while k != 0 do
if k is odd then
r = r * t mod n
t = t^2 mod n
k = floor(k / 2)
return r

