Asymptotic Notation

COMP202 Lectures 2022-02-03

This type of notation allows for the characterisation of the main factors affecting running time.

Big-O Notation

Given two positive functions (algorithms) $f(n)$ and $g(n)$, defined on non-negative integers, we say:

\[f(n) \text{ is } O(g(n))\]

or equivalently:

\[f(n) \in O(g(n))\]

if there are constants $c$ and $n_0$ such that:

\[\forall n\geq n_0, f(n)\leq c\cdot g(n)\]

We want to see what it takes to make $g$ be greater than $f$.

This can also be represented in the following graph:

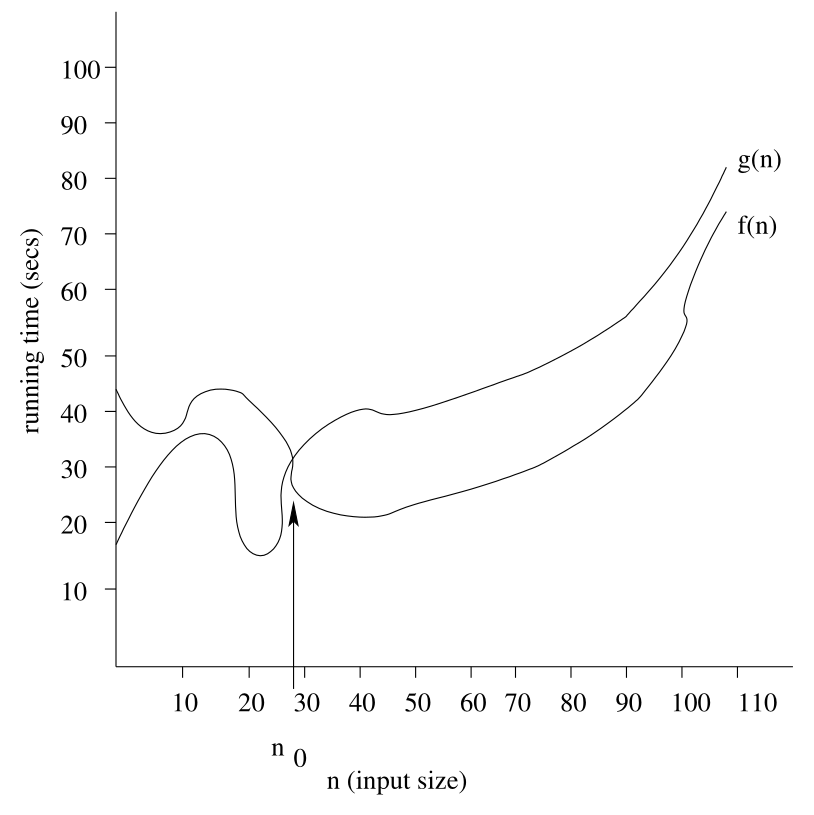
Big-O Example

Consider the example of:

\[7n - 4\in O(n)\]

To validate this we need to find constants $c$ and $n_0$ such that:

\[\forall n\geq n_0, 7n-4\leq cn\]

We could choose the values:

• $c=7$
• $n_0=1$

In order to satisfy the inequality we could have chosen any real numbeer $c\geq7$ and any integer $n_0\geq1$.

There are additional big-O examples in the slides.

$\Omega(n)$ & $\Theta(n)$ Notation

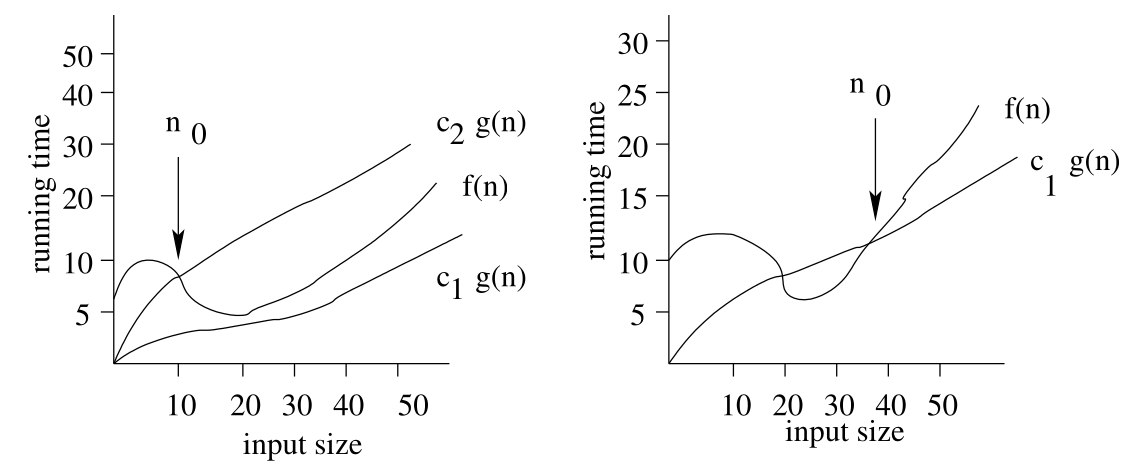
• We say that $f(n)$ is $\Omega(g(n))$ (big-Omega) if there are real constants $c$ and $n_0$ such that:

  \[\forall n\geq n_0 f(n)\geq cg(n)\]

• We say the $f(n)$ is $\Theta(g(n))$ (big-Theta) if $f(n)$ is $\Omega(g(n))$ and $f(n)$ is also $O(g(n))$.

You can see and example of this in the following graphs:

Renter’s Dilemma

Consider that to rent a film it costs $x$ but to buy it, it costs $10\times x$. We want to decide when would be the best time to buy the film.

Online vs. Offline Algorithms

• Online Setting - Requests arrive sequentially and upon arrival they must be dealt with immediately.
• Offline Setting - The entire sequence of events are given and the optimal solution must be chosen.

Competitive Analysis

This is the process of comparing a given online algorithm $A$ to an optimal offline algorithm $OPT$.

We can say that, given a sequence of requests $R=(r_1,r_2,\ldots,r_n)$, the costs of using either algorithm are calculated like so:

• cost($OPT,R$)
• cost($A, R$)

Algorithm $A$ is c-competitive, for some $c\geq1$, for $R$ if:

\[\text{cost}(A,r)\leq c\cdot \text{cost}(OPT,R)+b\]

for some constant $b>0$.

If $A$ is c-competitive for ever sequence $R$, then we say that $A$ is c-competitive:

• $c$ is the competitive ratio.

If $b=0$, then $A$ is strictly c-competitive.

Renters Dilemma Example

Consider the following strategy for an online algorithm:

You rent the film every time you want to watch it.

• This will cause you to spend $n\times x$ which could be up to $\frac {n\times x} {10}$ more pounds than is optimal.

A more optimal solution would be to rent 10 times and then buy the film.

• In this case you would spend at most 2 times more than an offline strategy. You can call this 2-competitive.

You can find an analysis of this at slide 50.