Catch-up Session 6
Power Sets
The power set $\text{Pow}\{A\}$ of a set $A$ is the set of all possible subsets. This includes the null set $\emptyset$ and the full set.
Each set in the power set follows this definition:
\[\{x\vert x\subseteq A\}\]Example
The power set $\text{Pow}\{A\}$ of a set $A=\{1,2\}$ is:
\[\{\emptyset,\{1\},\{2\},\{1,2\}\}\]For any set $A$:
\[\vert \text{Pow(A)}\vert =2^{\vert A\vert }\]Therefore:
\[\{x\vert x\in\text{Pow}(A)\}=\{\emptyset,\ldots\}\]Russell’s Paradox
People say that you can define a set just by defining the constraints of the set:
\[\{x\in\mathbb{R}\vert x<4,x\geq-1\}\]However statements written in this way are susceptible to paradoxes. For example the following paradox:
Everyone from Crete is a liar. (Said by a person from Crete)
Paradoxes in General
A paradox is a case that when expanded contains a contradiction.
Avoiding Paradoxes
To avoid paradoxes we should write the set definition in the following way:
\[\{x\in\ldots\vert \ldots\}\]This means that the set or value x should be taken from some other set.
They should not be written like this:
\[\{x\ldots\vert \ldots\}\]Venn Diagrams and Set Logic
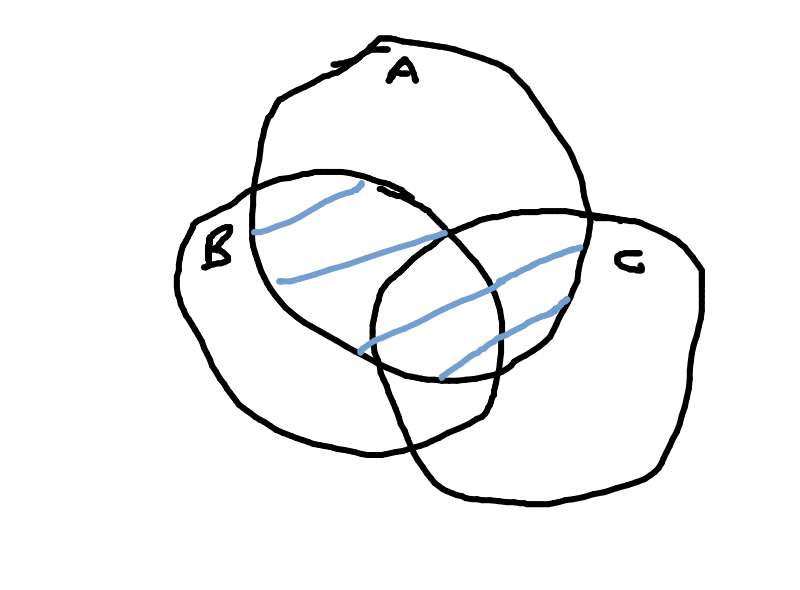
Draw the following as a Venn diagram: $A\cap (B\cup C)$
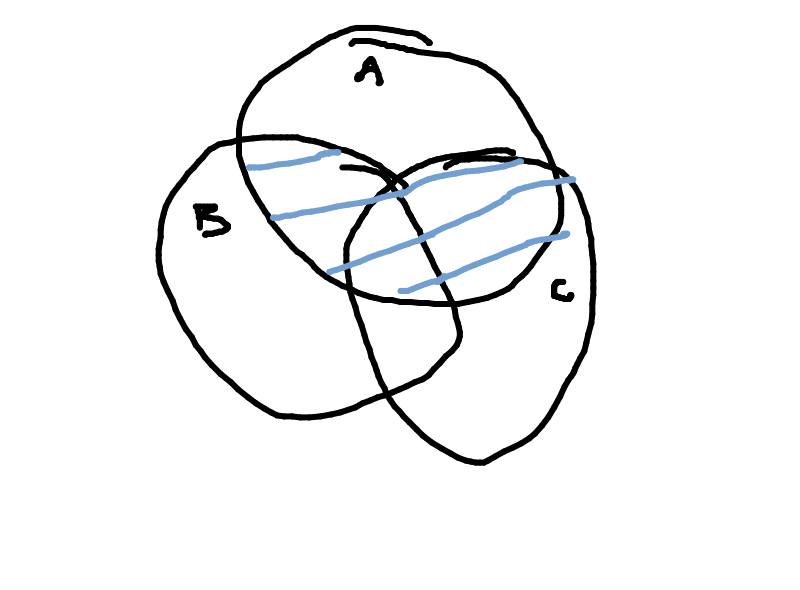
Draw the following as a Venn diagram: $(A\cap B)\cup(A\cap C)$