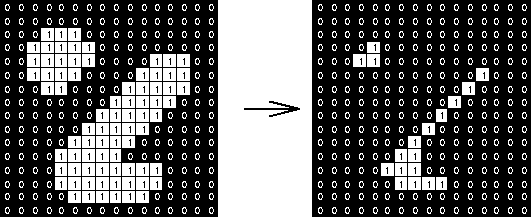Morphological Operations
Morphology is concerned with the shape of structures.
Morphological Erosion
The final image is a subset ($\subseteq$) of the original image.
Allows objects to shrink and separates objects & regions.
It is a pixel-by-pixel operation, sliding the structuring element (SE) at every pixel:
- If the origin of the SE coincides with a 0 (background pixel) of the image:
- There is no change, move the the next pixel.
- If th origin of the SE coincides with 1 (foreground pixel):
- Perform an
ANDoperation on all the pixels within the SE.
- Perform an
Pixel-by-pixel operations are very slow.
Erosion is expressed by the set operation:
\[A\ominus B\]where:
- $A$ - The source image.
- $B$ - The structuring element.
This is good for getting rid of salt noise (white spots) on images.
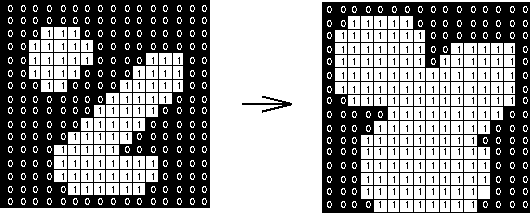
Morphological Dilation
This is the opposite of erosion, allowing objects to expand.
It is a pixel-by-pixel operation, sliding the structuring element (SE) at every pixel:
- If the origin of the SE coincides with a 0 (background pixel) of the image:
- There is no change, move the the next pixel.
- If th origin of the SE coincides with 1 (foreground pixel):
- Perform an
ORoperation on all the pixels within the SE.
- Perform an
This results in the maximum output of the local region of the structuring element.
Dilation is expressed by the set operation:
\[A\oplus B\]This is good for getting rid of pepper noise.
Other Morphological Operations
Morphological Opening
This is erosion followed by dilation with the same structuring element:
\[A\circ B = (A\ominus B)\oplus B\]This smooths contours and removes noise.
Morphological Closing
Dilation followed by erosion with the smae structuring element:
\[A\bullet B = (A\oplus B)\ominus B\]Joins nearby connected components together.
Morphological Boundary Extraction
We can get the boundary of an object by:
- Eroding with a suitable SE.
- Subtract this form the original image.
Extracting Connected Components
Extraction of connected components can be performed using morphological operation as an iterative procedure.
- Let $x_k$ denote the set of connected foreground pixels at the $k^{\text{th}}$ iteration.
- Start the procedure at one of the connected foreground pixels $x_0$.
- $x_0$ is known as the seed.
- Dilate this pixel: $x_0\oplus B$
-
To stop this dilation becoming connected to pixels which are not part of this component, perform a logical AND with the image:
\[(x_0\oplus B)\cap A\] - Use the resulting output as the seed for the next iteration.
- Repeat this until no more extractions can be made.
This can be expressed in the following steps:
-
Do for $k={1,\ldots}$:
\[x_k(x_{k-1}\oplus B)\cap A\] -
Until:
\[x_k=x_{k-1}\]
Region Filling
This closes holes in objects. It consists of the following steps:
-
Set:
\[x_0=1, x_x\oplus B\] -
Do for $k={1,\ldots}$:
\[x_k=(x_{k-1})\cap \bar A\] -
Until:
\[x_k = x_{k-1}\]
Hit-and-Miss Transform
This searches for images the structuring component in an image. It is given by:
\[A\otimes B=(A\ominus B_1)\cap(\bar A\ominus B_2)\]Where we have two structuring elements:
\[B_1\cap B_2=\emptyset\]Skeletonisation
This is the process for reducing foreground regions in a binary image to a skeletal remnant.
Let $A$ be an image and $B$ be a structuring element.
Let $(A\ominus kB)$ denote $k$ successive erosions of $A$ using $B$.
The the skeleton of an image $A$ is:
\[S(A)=\bigcup^K_{k=0}\left\{(A\ominus kB)-(A\ominus kB)\circ B\right\}\]- $K$ is the maximum number of iterations before the image is eroded to nothing.
Top-Hat
The difference between the image $I$ and the opened version of the image $I$:
\[T(I)=I\hat\circ s=I-I\circ s\]This returns object of an image that are:
- Smaller than the SE
- Brighter than their surroundings.
This highlights peaks.
Bottom-Hat
The difference between the closed version of the image and the image $I$:
\[B(I) = I\hat\bullet s=I\bullet s-I\]Returns objects of an image that are:
- Smaller than the SE
- Darker than their surrounding.
This highlights valleys.