Nearest Neighbour Classifier - 2

COMP111 Lectures 2020-12-10

$k$-Nearest Neighbour Classifier

For $x$ to be classifier find $k$ nearest $x_{i_1},\ldots,x_{i_k}$ in the training data.

Classify $x$ according to the majority vote of their class labels.

For $k=3$:

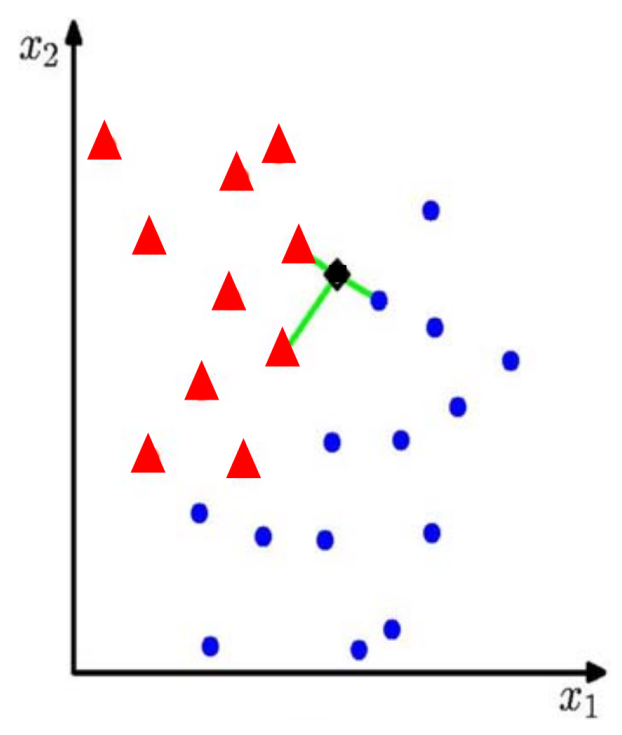
The $k$ represents the number of closest labels you are taking into account.

1: Input: training data (x0, L(x0)), ... , (xn, L(xn))
2:     new x ∈  X to be classified
3:
4: for i = 0 to n do
5:     Compute distance d(x, xi)
6: endfor
7: Let xi1, ... , xik be the list of items such that
8:     d(x, xij) is among the k smallest distances
9: return label L which occurs most frequently in L(xi1), ... , L(xik) (majority vote)

Learning a “good” $k$

To learn a “good” $k$ divide labelled data into training data $T$ and validation data $V$.

This will result in the following two subsets of the labelled data:

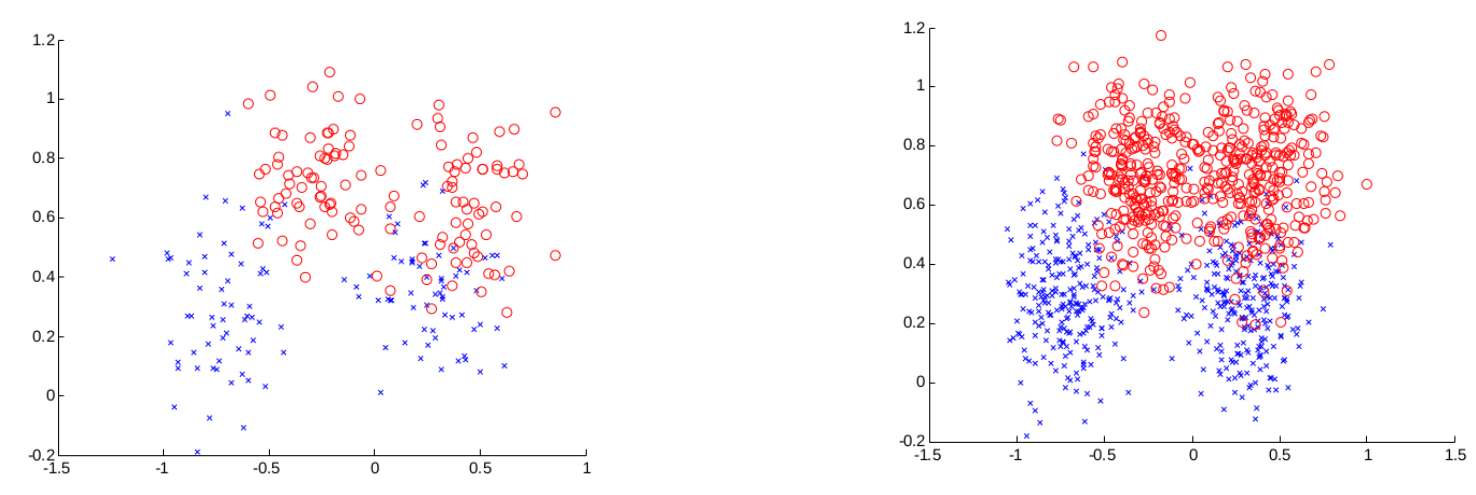
The left is the training data and the right is the validation data.

The classification error of a classifier $f$ on a set of data items is the number of incorrectly classified data items divided by the total number of data items.

We are saying here that we want a $k$ such that new items added have the least classification error.

Let:

• $f_1$ be the 1-nearest neighbour classifier obtained from the training data $T$.
• $f_2$ be the 2-nearest neighbour classifier obtained from the training data $T$.
• and so on for $3,\ldots,m$.

Choose $f_k$ for which the classification error is minimal on the validation data (not the training data).

Generalisation

• The aim of supervised learning is to do well on test data that is not know during learning.
• Choosing the values for parameters (here $k$) that minimise the classification error on the training data is not necessarily the best policy.
• We want the learning algorithm to model true regularities in the data and ignore noise in the data.

Training and Validation Data - $k=1$

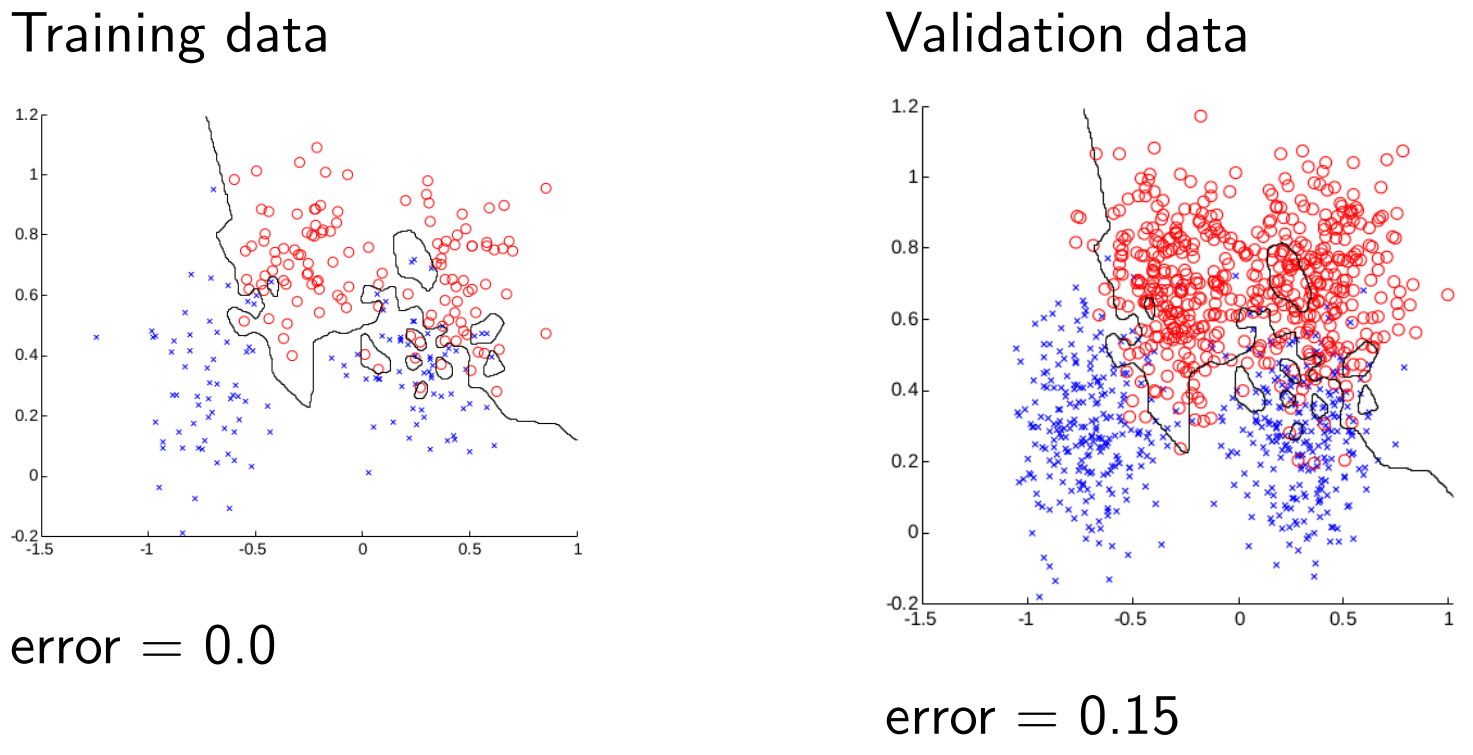
If we chose the value that was best for the training data then we can see here that we would almost always go for $k=1$. However, we want to be good generally so we optimise $k$ for the test data.

Training and Validation Data - $k=7$

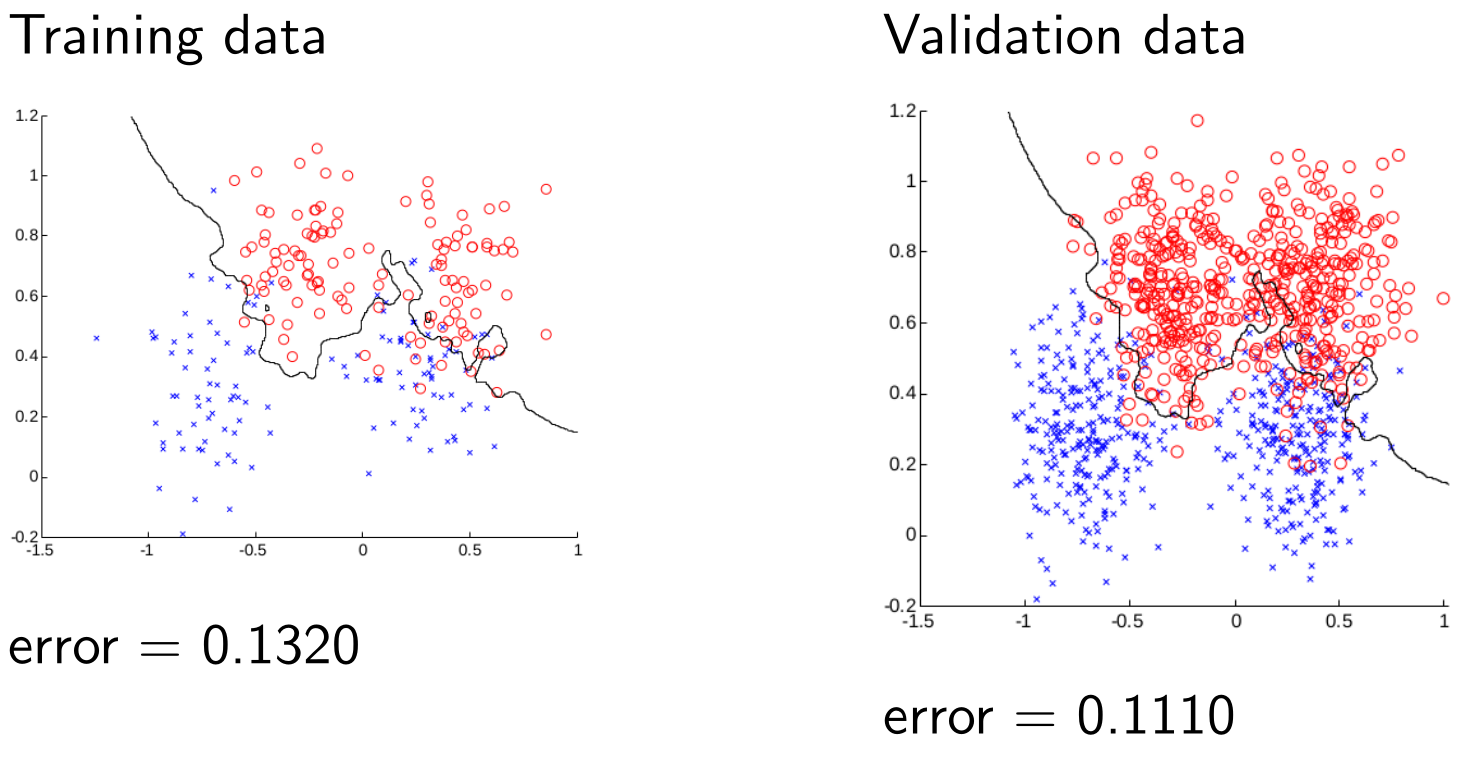
You can see that although the error of the training data goes up the “general” error (on the validation data) goes down. We want to increase $k$ to minimise this value.

The line also gets smoother as $k$ increases as it is interpolating the data and removing noise.

Properties and Training

As $k$ increases:

• Classification boundaries become smother (possibly reflecting regularity in the data.
• Error on the training data can increase.

Summary

Advantages

• $k$-nearest neighbour is simple but effective.
• Decision surface can be non-linear.
• Only a single parameter, $k$, easily learned by cross validation.

Disadvantages

• What does nearest mean?
  • Need to specify a distance measure.
• Computational cost.
  • Must store and sear through the entire training set at test time.