Probability of the Union of Events
Disjoint Events
Assume that $E _1,\ldots,E_n$ are mutually disjoint events. So $E_i\cap E_j=\emptyset$ whenever $i\neq j$.
Then,
\[P(\bigcup_{i\leq i \leq n}E_i)=\sum_{1\leq i\leq n}P(E_i)\]Example - Three Dice
Suppose that I roll a fair die three times:
- $S$ is the set of dequences of lengh three over $\{1,\ldots,6\}$ (or $\{1,\ldots,6\}^3$).
- $P(x)=\frac{1}{6\times6\times6}=\frac{1}{216}$ for all $x\in S$.
What is the probability that I roll at least one 6?
Let $E_1$: even that 1^st roll is a 6, $E_2$: event that 2^nd roll is a 6; $E_3$: event that 3^rd roll is a 6.
This means that we would like to know:
\[P(E_1\cup E_2 \cup E_3)\]Computing the Probability of a Union of Three Sets
\[\begin{aligned} P(A\cup B \cup C)=&P(A)+P(B)+P(C)\\ &-P(A\cap B)-P(A\cap C)\\ &- P(B\cap C)+P(A\cap B \cap C)\\ \end{aligned}\]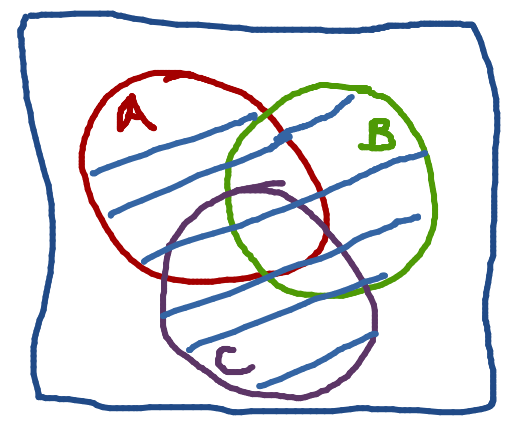
Additionally:
\[\begin{aligned} \vert A\cup B \cup C\vert =& \vert A\vert + \vert B\vert +\vert C\vert\\ &-\vert A\cap B\vert -\vert A\cap C\vert -\vert B\cap C\vert\\ &+\vert A\cap B \cap C\vert \end{aligned}\]Example Continued
- $E_1$: even that 1^st roll is a 6.
- $E_2$: event that 2^nd roll is a 6.
- $E_3$: event that 3^rd roll is a 6.
We can calculate the answer with the equation from earlier:
\[\begin{aligned} P(E_1\cup E_2 \cup E_3)=&P(E_1)+P(E_2)+P(E_3)\\ &-P(E_1\cap E_2)-P(E_1\cap E_3)\\ &- P(E_2\cap E_3)\\ &+P(E_1\cap E_2 \cap E_3)\\ =&\frac{36}{216}+\frac{36}{216}+\frac{36}{216}\\ &-\frac{6}{216}-\frac{6}{216}-\frac{6}{216}\\ &+\frac{1}{216}\\ =&\frac{91}{216}\approx0.42 \end{aligned}\]