Nearest Neighbour Classifier - 1

COMP111 Lectures 2020-12-10

This classifier is an example of similarity based classifiers.

Similarity Measures

Assume that we can measure the similarity between items in the training data $\mathcal X$. For example:

• One could measure how similar two emails are by counting the number of words from the English dictionary they both contain and compare it to the number of words only one email contains.

• Similarity also plays a role when recognising hand-written digits (1 is rather similar to 7 which makes them harder to distinguish than 1 and 8). A possible measure for $28\times28$ pixel images $a$ and $b$ is given by:

  \[\sqrt{\sum_{1\leq i,j\leq 28}(a_{ij}-b_{ij})^2}\]
• To classify a new data item $x$, a similarity-based classifier considers the classification of the items most similar to $x$ in the training data $\mathcal X$ can classifies $x$ accordingly.

Distance Measures

We measure similarity between data items using a distance measure $d$ which assigns to data item $x$, $x’$ a non-negative number:

\[d(x,x')\in\Bbb{R}\]

$d(x,x’)$ is called the distance between $x$ and $x’$

One typically requires that $d$ satisfies the following equations for metric spaces:

• $d(x,y)=0$ if and only if $x=y$ (identity indiscernibles).
  • This means that if the distance is zero then they are the same thing.
• $d(x,y)=d(y,x)$ (symmetry).
  • This means that opposites have equal distance.
• $d(x,y)+d(y,z)\geq d(x,z)$ (triangle equality).
  • This means that the distance from $x\rightarrow z$ must be greater that the distance of $x\rightarrow y\rightarrow z$.

Distances for Items with Numerical Features

Numerous distance measures have been introduced. Of particular importance is the Euclidean distance which gives, in the two and tree dimensional case, the length of the straight line between points.

The Euclidean Distance:

\[d((e_1,\ldots,e_n),(f_1,\ldots,f_n))\]

between $(e_1,\ldots,e_n)$ and $(f_1,\ldots,f_n)$ is:

\[\sqrt{\sum^n_{i=1}(e_i-f_i)^2}\]

For $n=1$:

\[d(e,f)=\sqrt{(e-f)^2}=\left\vert e-f\right\vert\]

For $n=2$:

\[d((e_q,f_q),(e_2))=\sqrt{(e_1-f_1)^2+(e_2-f_2)^2}\]

This is an application of the Pythagorean theorem for straight line distances.

Distances for Items with Non-Numerical Features

Consider qualitative data such as:

Day	outlook	temp	humidity	wind	play
D1	sunny	hot	high	weak	No
D2	sunny	hot	high	strong	No
D3	overcast	hot	high	weak	Yes
D4	rain	mild	high	weak	Yes

What should the distance between $D1$ and $D2$ (as far as the weather is concerned) be?

A natural distance measure in this case is the matching distance between values of features. This distance is equal to the number of features where $Di$ and $Dj$ do not coincide.

This can give:

• $d(D1,D2)=1$
• $d(D1,D4)=2$

Nearest Neighbour Classifier

Assume the data in $\mathcal C$ come with a distance measure $s(x,x’)\in\Bbb{R}$ which states how similar $x,x’\in\mathcal X$ are. Then the nearest neighbour classifier works as follows:

Given training data:

\[(x_1,L(x_1)),\ldots,(x_n,L(x_n))\]

for a new $x\in\mathcal X$ to be classifier, let $x_i$ be the element of the training set that is nearest to $x$:

\[d(x,x_i)\leq d(x,x_j), \text{for all } x_j\neq x_i\]

Then define the value $f(x)$ of the classifier $f$ by setting:

\[f(x)=L(x_i)\]

1: Input: training data (x0, L(x0)), ... , (xn, L(xn))
2:     new x ∈ X to be classified
3: for i = 0 to n do
4:     Compute distance d(x, xi)
6: endfor
7: return L(xi) such that d(x, xi) is minimal

A nearest neighbour classifier partitions $\mathcal X$ into regions. boundaries are equal distance from training points:

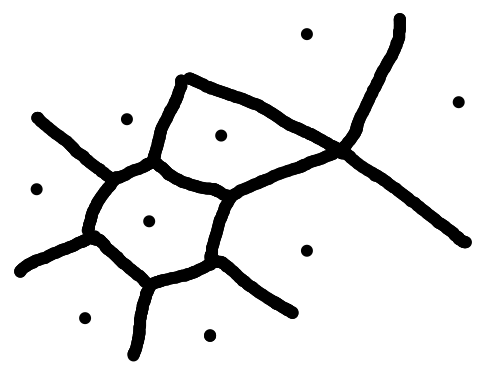
We can then split the classes and follow the lines along the split of the two regions. For a new item we would then classify it by the region that it falls into.

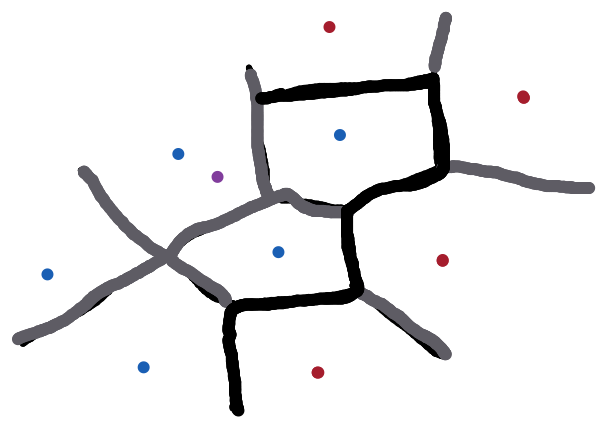
In this case you can see that the purple item falls into the blue class as it is in that section.

Problems

• The nearest neighbour classifier is very close to the training data.
• It does not generalise the training data.
  • If the training data is noisy, then the classifier is noisy as well.
    • If a spam email is erroneously labelled as non-spam, then all similar emails will also be classified as non-spam.