Searching & Inserting in B+ Trees

COMP207 Lectures 2021-11-16

There is a visualisation tool for B+ trees available at https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html.

Single vs Multi-Level Indexes

• Single Level Index - Stores in a single list.
• Multi-Level Index - Distributes across different layers.

B+ Tree Leaves (Idea)

$a_1$	$a_2$	$\ldots$	$a_n$
Points to tuples with value $a_1$.	Points to tuples with value $a_2$		Points to tuples with value $a_n$.	Next Leaf

$n$ is chosen such that a node fits into a single disk block:

• Disk Block Size - 512 byte
• Values - 4 byte integers
• Pointers - 8 bytes

With the above example $n=42$ as:

\[\begin{aligned} 512&\geq42(8+2)+8\\ 512&<43(8+4)+8 \end{aligned}\]

B+ Tree Inner Nodes (Idea)

$a_1$	$a_2$	$\ldots$	$a_n$
Points to a nodes for values $<a_1$.	Points to nodes for values $\geq a_1$ and $<a_2$		Points to nodes for values $\geq a_{n-1}$ and $<a_n$	Points to node for values $\geq a_n$

Pointers point to B+ tree nodes at the level below. $n$ is chosen as before.

B+ Tree Leaves (Actually)

• Not all the fields have to be used.
• Fields are filled from left to right.

$a_1$	$a_2$	$\ldots$	$a_i$	Unused	Unused
Points to tuples with value $a_1$.	Points to tuples with value $a_2$		Points to tuples with value $a_u$.	Points Nowhere	Next Leaf

Ensure that at least $\lfloor \frac{n+1}2\rfloor$ pointers are used (unless this is the only leaf).

To follow with the online tool, we count the next leaf pointer as a pointer, even if there is none.

B+ Tree Nodes (Actually)

• Not all the fields have to be used.
• Fields are filled from left to right.

$a_1$	$a_2$	$\ldots$	$a_i$	Unused	Unused
Points to a nodes for values $<a_1$.	Points to nodes for values $\geq a_1$ and $<a_2$		Points to nodes for values $\geq a_{i-1}$ and $<a_i$	Points to node for values $\geq a_i$	Points Nowhere

Where:

• $a_i$ - Number is smallest number in child-sub-tree slightly to the right.

Ensure that at least $\lceil \frac{n+1}2\rceil$ pointers are used (the root must use $\geq 2$ pointers).

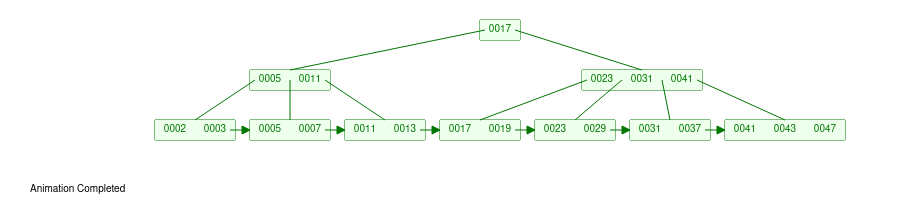
B+ Tree Index

A B+ tree index of the prime numbers through 47 looks like the following:

Searching Values

To find the pointer to the rows with value $v$:

1. Start at the root of the B+ tree.
2. While the current node is a non-leaf node:
   • f $v<a_1$, proceed to the first child of the node.
   • Otherwise find the largest $i$ with $a_i\geq v$ and proceed to the associated child node.
3. If the current node is a leaf:
   • If $v$ occurs in the leaf, follow the associated pointer.
   • If $v$ does not occur in the leaf, return “$v$ doesn’t exist in the index”.

The running time is:

\[O(h\times\log_2n)\]

where $h$ is the height of the B+ tree.

The real running time is:

\[O(h\times D)\]

where $D$ is the time for a disk operation.

Inserting Values

To insert a new value/pointer pair:

1. Find the leaf that should contain the value.
2. If the leaf is not full, insert the key value pair at a suitable location.
3. If the leaf is full:
   1. Split the leaf to make space for the new value/pointer pair and move half of the pointers to the new node.
   2. Insert the value/pointer pair
   3. Connect the leaf to a suitable parent node (which might incur the creation of a new node).

The running time is:

\[O(h\times\log_2n)\]

where $h$ is the height of the B+ tree.

The real running time is:

\[O(h\times D)\]

where $D$ is the time for a disk operation.