UoL CS Notes
Menu

Neural Networks Introduction

ELEC320 Lectures

Brains and (A)NNs

The brain is:

  • Highly Complex
  • Non-linear
  • Massively parallel

ANNs (artificial neural networks) are biologically inspired analogues of the brain and are based on primitive neuron components.

Neuron Structure

Synapses
Facilitate learning via creation of new, and modification of existing ones.
Axons
Signal transmission structures
Dendrites
Receptive structures

We can simulate a neuron with the following strucutre:

graph LR
x1 -->|w1| n[Neuron]
x2 -->|w2| n
xn -->|wn| n
n --> output

Each input has a weight and is summed as it enters the neuron to form the output:

\[\sum^N_{i=1} x_i w_i\]

We can then apply a threshold to the output if we want a binary output from the neuron.

Advantages of ANNs

  • Non-linearity
  • Input-to-output Mapping
  • Adaptivity
    • NN can be retrained to adapt to solve a changing task or be adapted to a similar one.
  • Evidential Response
    • A confidence can be provided as to whether the output is correct.
  • Contextual Information
    • Knowledge is integrated into the network. Each neuron is affected by all others; local processing and global awareness.
  • Fault Tolerance
    • When small damage occurs, the network usually degrades gracefully.
  • Uniformity of Analysis and Design
    • NNs are composed of similar components. This allows for modularity and use of mathematics for learning and network analysis.
  • Neuro-biological Analogy
    • As the system is already implemented in nature. The system is proven.

Using Machine Learning

Consider we want to use a NN to classify fish based on their lightness and width. We can use the following feature vector to represent each fish:

\[x = [x_1,x_2]^\top\]

Where:

  • $x_1$ is lightness
  • $x_2$ is width

Based on a set of training samples, the neural network could produce the following decision boundary by use of it’s weights:

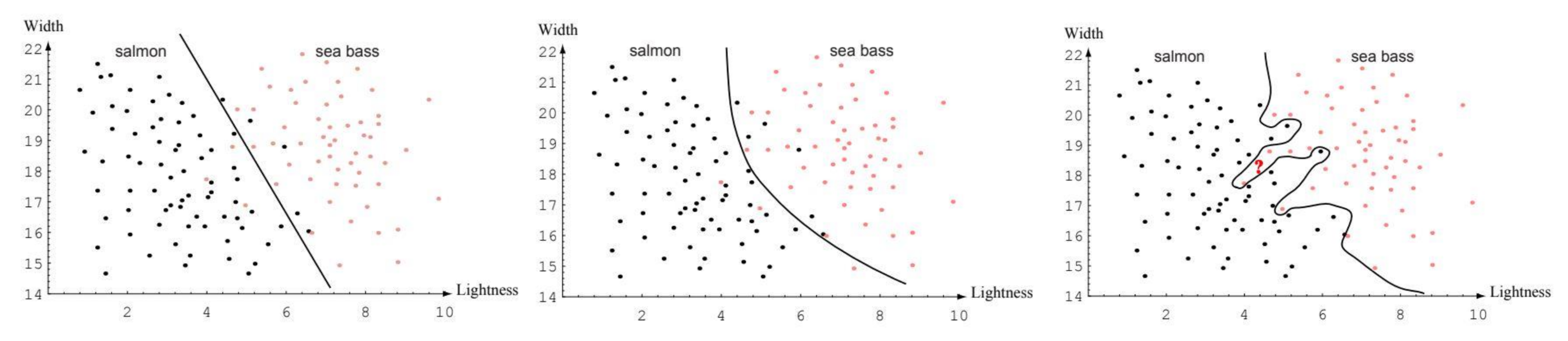
decision boundary

From this training we may observe the following phenomenon:

  • Under-fitting
    • A machine learning model is not complex enough to accurately capture relationships between a dataset’s features and the target variable.
  • Over-fitting
    • The model is too closely fit to a limited set of data points and does not generalise well to unseen data points.