Complex Valued Functions - 2 (Integral Calculus)
In real integration this can be likened to measuring the area under the graph. This is not true for complex numbers.
Complex integration can be useful in finding the average case of an algorithm.
Integrating Complex Numbers
Suppose $f:\Bbb C\rightarrow \Bbb C$ and $p,q\in \Bbb C$.
How do we interpret:
\[\begin{aligned} \int^q_pf(z)dz=&\int^q_p\text{Re}(f(z))dz\\ &+i\int^q_p\text{Im}(f(z))dz \end{aligned}\]The complex numbers are not ordered, so (unlike the reals) we cannot think in terms of area between $p$ and $q$.
We can think in terms of: move from the point $p$ to the point $q$ in the complex plane.
Curves and Contours
Suppose we have two points $p,q$ in the complex plane.
Intuitively, we understand how to connect how to connect these by drawing some curve from one to the other:
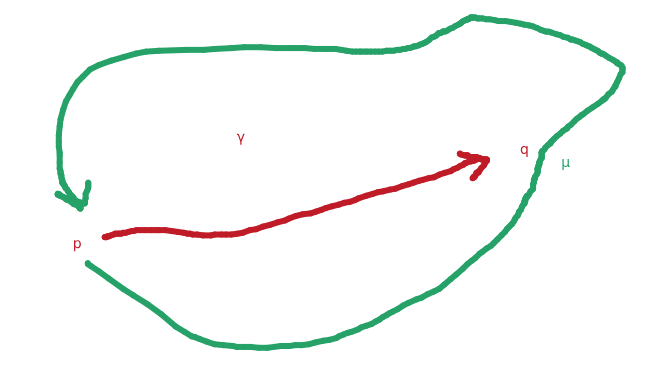
Parameterised Curves
We can move between points by describing the path to use (and its direction). This was $\gamma$ and $\mu$ in the example.
When we do this the integral concerned is defined as:
\[\int_\gamma f(z)dz\]The difference here is that we aren’t giving bounds but the curve we are integrating with respect to.
In the special case of closed curves (when the start and end coincide) we have so-called contour integrals:
\[\oint_\mu f(z)dz\]Parametrisation of Curves
We have an interval we are interested in: $[\text{Re}(p),\text{Re}(q)]$.
As before $p$ is the start point and $q$ is the end point.
How do we describe moving along a path $\gamma$?
-
By using a function $c:\Bbb R\rightarrow \Bbb C$ for which:
\[c(\text{Re}(p))=p;c(\text{Re}(q))=q\]These properties must be satisfied. The resultant $p$ and $q$ are complex numbers.
We can split this above function into both real and imaginary parts:
\[x(t) = \text{Re}(c(t));y(t)=\text{Im}(c(t))\]This means that for any $t:\text{Re}(p)\leq t\leq \text{Re}(q)$:
\[c(t) = x(t)+i\times y(t)\]
This is called a parametrisation of the curve.
Application
It can be shown that, when the function $c:\Bbb R \rightarrow \Bbb C$ parametrises the curve $\gamma$ joining $p$ and $q$ then:
\[\int_\gamma f(z)dz\equiv\int_{\text{Re}(p)}^{\text{Re}(q)}f(c(t))c'(t)dt\]The domain of the right hand integral is the reals. This means that we can use standard integration by writing:
\[\begin{aligned} &\int_{\text{Re}(p)}^{\text{Re}(q)}\text{Re}\left(f(c(t))c'(t)dt\right)\\ &+\int_{\text{Re}(p)}^{\text{Re}(q)}\text{Im}\left(f(c(t))c'(t)dt\right) \end{aligned}\]Example
Two examples are given from slide 8 of the lecture slides.
This example is also run through from 10:29-16:24:
The first is for an open curve and the second is for a close curve.
Counting Objects
In computer science we might want to find exact or asymptotic estimates for the number of object of a particular type having size $n$.
Two tools that are often used are the notion of a generating function and a result called the (generalised) Cauchy integral formula.
Generating Function
Suppose we write:
\[G(z)=\sum^\infty_{n=0}a_nz^n\]The coefficient of $z^n$ describes the number of interest.
We can often manipulate this sum to find a closed form.
Example
Consider counting the number of binary trees that have a certain number of leaves. We will use the above function as our generating function.
A binary tree is either a single root node ($n=0$) or a root node and two sub-trees, whose number of leaves added is $n$.
After some manipulation this allows $B(z)$ to be written as:
\[B(z)=\frac{1-\sqrt{1-4z}}{2z}\]If we can find $z^n$ easily then we are done.
The Generalised Cauchy Integral Formula
If we want to find $a_n$ from a closed form (say $g(z)$ for $G(z)$ its generating function) we could differentiate $g(z)$ $n$ times and extract the value we need. Or, letting $g^{(n)}(z)$ denote this derivative:
We can use the generalised Cauchy integral theorem. Choose a closed contour $C$ then:
\[g^{(n)}(z)=\frac{n!}{2\pi i}\oint_C\frac{g(\beta)d\beta}{(\beta - z)^{n+1}}\]and just evaluate this at $z=0$.
Summary
This lecture doesn’t cover significant details of all aspects in this lecture.
- Complex analysis is important in specialised areas such as:
- Algorithmics - counting.
- Estimating hard to count quantities.
- Average-case (as opposed to worse case) studies.