Relational DB Quality - 2

COMP107 Lectures 2020-12-09

Normalisation

This is the mathematical process of reducing linked tables to a normal form.

Functional Dependencies

This is a formal tool for analysis of relational schemas. The theory of functional dependencies allows us to describe as detect issues in precise terms.

A functional dependency is constraint between two sets of attributes from the database.

Legal relation states in the DB are only those that satisfy the functional dependency constraints.

One attribute $A$ is functionally dependent on another attribute $B$ if the value of $B$ uniquely determines the value of $A$.

• Notation: $B\rightarrow A$
  • $B=\{\text{StaffNumber}\}$ $\rightarrow A =\{\text{FirstName, Surname}\}$

$B\rightarrow A$ meant that any two tuple with the same value for $B$ must have the same value for $A$.

• Why isn’t this achieved with the primary key?
  • Because of join operations.

Join Operations

In order for two tables to be joined the primary key and the foreign keys must match.

From the Department table, given that the Department is the primary key, we can have the functional dependency:

\[B=\{\text{Department}\}\rightarrow A=\{\text{Address}\}\]

You can see in the table that $B\rightarrow A$ holds true as each address has a static matching department:

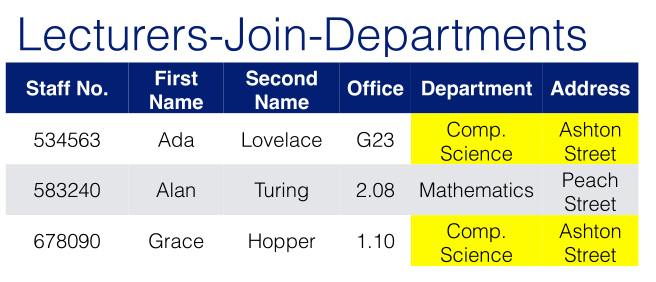
This constraint must also hold in any result of a query.

Diagrammatic Notation for Functional Dependencies

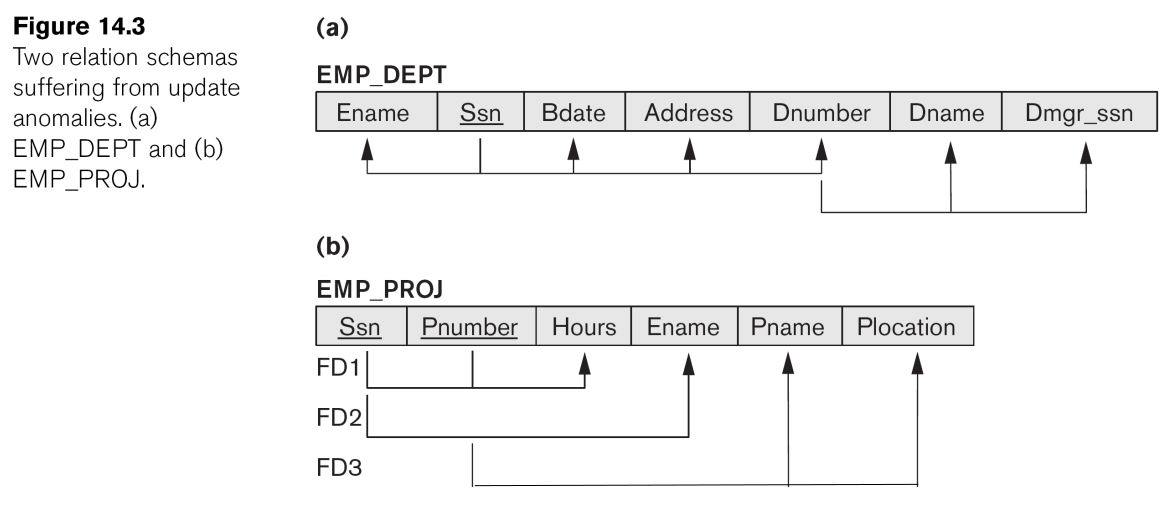
Normal Forms

Normalisation is a process, proposed by Codd in 1972, taking a relation through a set of tests to “certify” whether or not it belongs to a certain normal form.

• A normal form describes a set of properties that a relation must satisfy.
• Expressed in terms of which functional dependencies are allowed.

In the normalisation process, unsatisfactory relations are transformed to remove violations of the normal form rules.

• May involve decomposing a relation into smaller ones satisfying the rule.
• The attributes which violate the dependency are removed from the relation to create a new one.

A database schema is in normal form if all of its relations are in normal form.

Based on functional dependencies:

• 1st Normal Form (1NF)
• 2nd Normal Form (2NF)
• 3rd Normal Form (3NF)
• Boyce-Codd Normal Form (BCNF)

Based on “multi-valued” and “join” dependencies:

• 4th and 5th Normal Forms (4NF, 5NF)

Each NF extends the previous (so a relation in 3NF is also in 2NF and 1NF).

1NF

The domain of an attribute must include only atomic (simple, indivisible) values and the value of any attribute in a tuple must be a single value from the domain of that attribute.

• So: no sets (multivalued), no composite attributes.

Interesting for historical reason, now in the very definition of a relation.

Techniques to achieve First Normal Form:

1. Remove the violating attributes and place them in separate relations.
2. Use several atomic attributes (this will introduce many null attributes).
3. Expand the key (this will introduce redundancy!).

This is just moving multi-valued and non-atomic attributes to a new column or a linking table. This table:

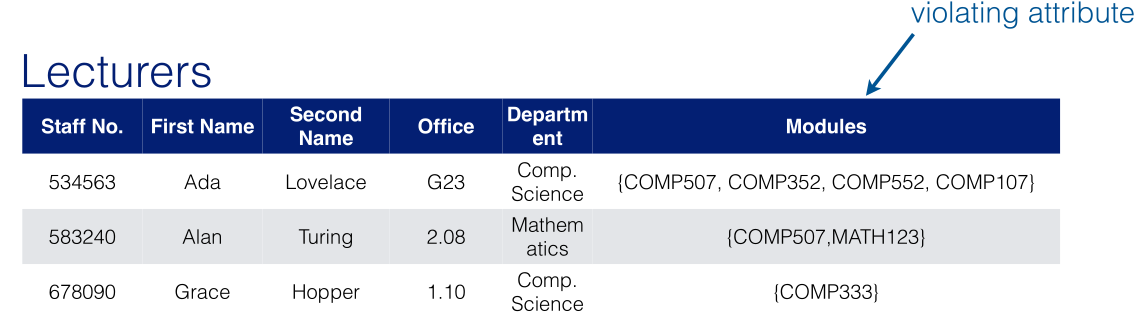
may become this table:

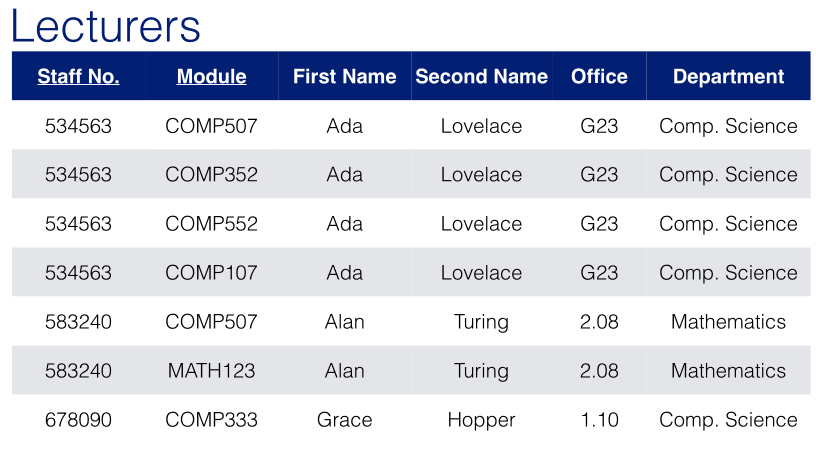
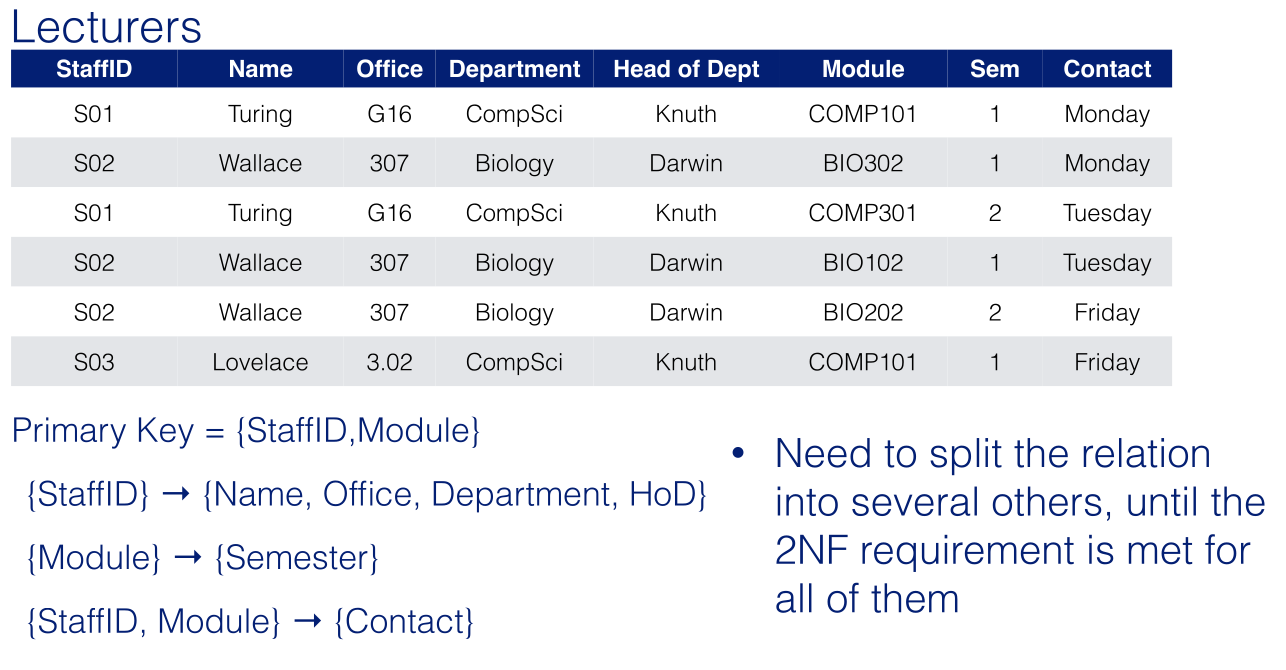
2NF

Concentrates on the primary key. A relation is in second normal form if:

1. It is in 1NF
2. All of its non-prime attributes are fully functional dependent on the primary key.

The second requirement means that all of the primary key should be used in order to determine the value of every other attribute:

• One should not be able to identify any values in any other attribute using only part of the primary key.
• This only has sense if the primary key comprises several attributes.

This will make the following table into the next:

3NF

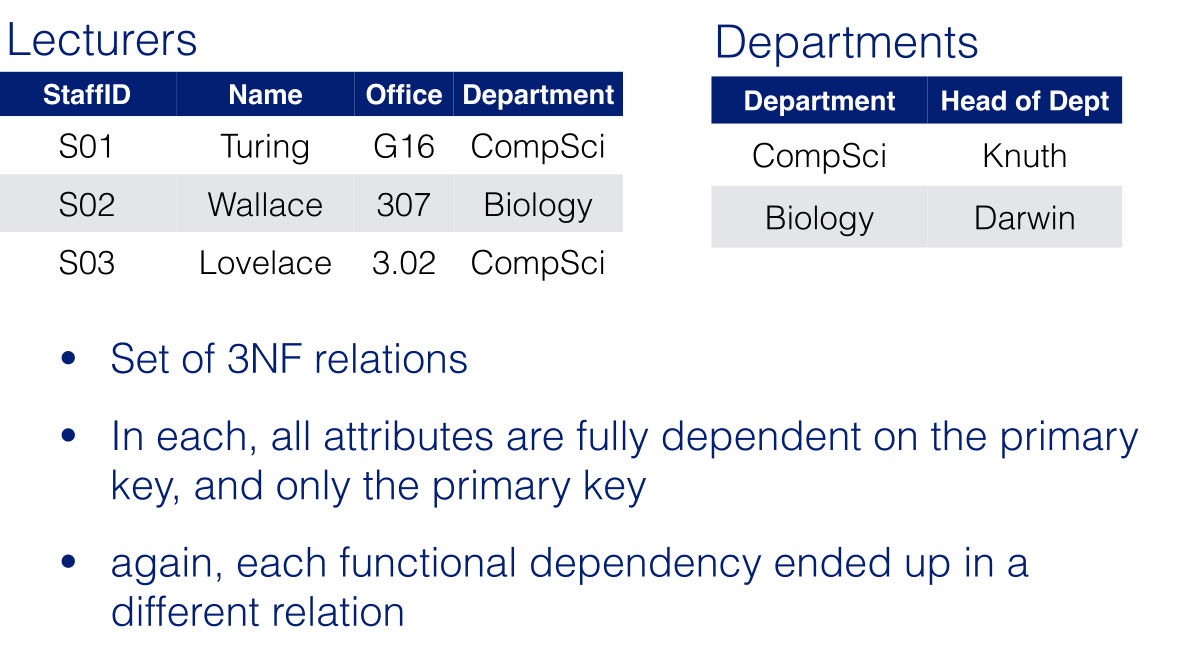
Concentrates on what is NOT a key. A relation is in third normal form if:

1. It is in 2NF
2. It is in second (and hence in first) normal form.
3. There are no transitive dependencies.

Two sets of attributes A and B are transitively dependent if there is another set of attributes C that is not a subset of any key such that A depends on C and C depends on B.

• The second requirement means that a non-key field must be solely dependent on the primary key.
• Cannot have that the key determines a set of attributes which in turn determines another set of attributes.

Dependent on the key the whole key and nothing but the key.

Beyond 3NF

3NF is not enough to normalise a table with relational constraints (N:M); this is a problem for a higher level of normalisation.

Boyce-Codd Normal Form (BCNF)

A relation is in Boyce-Codd Normal Form (BCNF) if:

1. It’s in 3NF.
2. Every time there is a non-trivial dependency $X\rightarrow A$ then $X$ is a super-key.

The relation in the example is not in BCNF because $\text{Tutor}\rightarrow \text{Department}$ holds, but Tutor is not a super-key.

For this example:

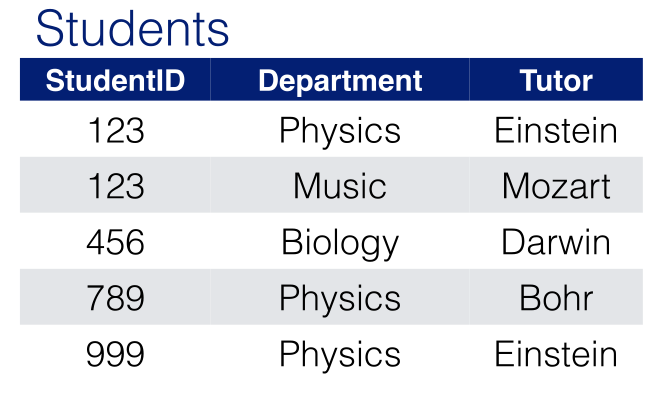
all of the following options are all equally BCNF:

1. $R1=\{\underline{\text{Student,Tutor}}\}$ and $R2=\{\underline{\text{Student,Department}}\}$
2. $R1=\{\underline{\text{Tutor}},\text{Department}\}$ and $R2=\{\underline{\text{Student,Department}}\}$
3. $R1=\{\underline{\text{Tutor}},\text{Department}\}$ and $R2=\{\underline{\text{Student,Tutor}}\}$

No mater which one we choose we lose track of the functional dependency $\{\text{StudentID, Department}\}\rightarrow \text{Tutor}$

Summary

If a database has been informally designed (e.g. without an ER model), normalisation ensures that undesirable dependencies have not been built in.

Normalisation does not remove all redundancy, it can only remove some unwanted redundancy.

• The one which can be removed by splitting relations.

Normalisation does not guarantee absence of spurious tuples.

Also, a normalised database has typically more relations.

• It may be desirable to relax normalisation to improve performance.