Algorithm Efficiency - 1

COMP108 Lectures 2021-02-17

Efficiency matters as we want to make more ambitious code to leverage increases in computational power. If we didn’t optimise code then we’d be wasting resources.

Time Complexity Analysis

Timing execution time is not enough as it is not reproducible and wastes time.

We should identify some important operations and count how many times these operation need to be executed.

We can then change the input size and see how the time the algorithm takes changes.

Data vs Speed Increase

Assume this initial scenario:

• An algorithm takes $n^2$ comparisons to sort $n$ numbers.
• We need 1 second to sort 5 numbers (25 comparisons).

Now suppose that Computing speed increases by a factor of 100:

• This means in 1 second we can now do 2500 comparisons.
• This gives a result of 50 numbers vs the original 5.

We show here that an $n^2$ comparison algorithm gives a 10 times speed increase with a raw 100 times speed increase.

Important Operations

Here is an algorithm:

sum = 0
i = 1
while i <= n do
begin
	sum = sum  + i
	i++
end 
output sum

The important operation of summation is addition.

For this algorithm we need $2n$ additions (dependant on the input size of $n$).

Which Algorithm is Fastest?

This question may be dependant on the input size you may want to use several algorithms:

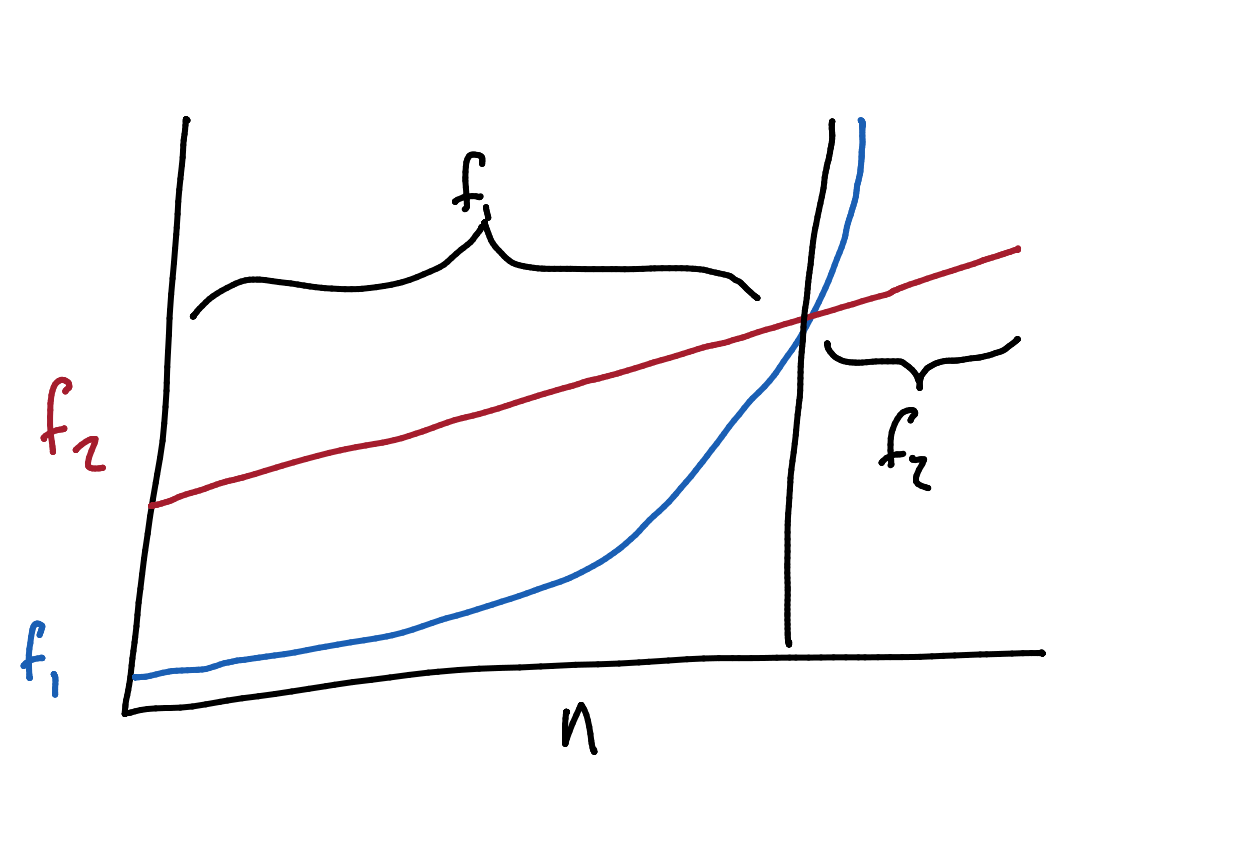
• $f_1(n) = n^2 -3n+6$
• $f_2(n) = 50n+20$

Generally you would want to choose the most efficient algorithm for when the input is maximal. In this example you would choose $f_2(n)$.

Growth Rate

Here are functions ordered by their growth rate:

• Constant
  • 1
• Logarithm
  • $\log n$
• Polynomial
  • $\sqrt n$
  • $n$
• Polynomial Logarithm (In-between each polynomial.)
  • $n\log n$
• Polynomial
  • $n^2$
  • $n^3$
• Exponential
  • $2^n$

In computer science $\log$ refers to $\log_2$.

Other Hierarchies

Comparing $\log^3n$ and $n$.

Identity: \(n\equiv 2^{\log_2n}\)

As $\log^3n$ is polynomial in terms of $\log n$ and $n$ (by the identity) is exponential in terms of $\log n$ the former is lower in the hierarchy.

Similarly, $\log^kn$ is lower than $n$ in the hierarchy, for any constant $k$.

Big-O Notation

\(f(n) =O(g(n))\)

Read as $f$ of $n$ is of order $g$ of $n$.

Roughly speaking, this means that $f(n)$ is at most a constant times $g(n)$ for all large $n$:

• $2n^3=O(n^3)$
• $3n^2=O(n^2)$
• $2n\log n=O(n\log n)$
• $n^3+n^2=O(n^3)$

When we have an algorithm, we can then measure its time complexity by:

• Counting number of operations in therms of the input size.
• Expressing it using big-O notation.